Coûts de production
Introduction
Thème du chapitre: l’approche classique de la firme et de la production:
- La relation entre technologie de production et les coûts;
- Les objectifs de l’entreprise canonique et l’ajustement de ses choix;
- La relation croissante entre quantité et prix sur un marché;
- La distinction entre l’offre d’une entreprise et celle du marché du produit;
- La concurrence parfaite, la libre entrée et la condition de zéro profits;
- Horizon temporel: la distinction entre court et long terme;
- Passer de la concurrence parfaite à la concurrence imparfaite.
Entreprise
Un agent qui produit un bien ou un service;
- Ses ventes génèrent des recettes;
- La production du bien/service est coûteuse.
- Elle cherche à maximiser son “profit” (exclut donc les institutions à but non lucratif).
- Approche de Coase: L’entreprises sert à minimiser les coûts de transaction entre propriétaires de “facteurs de production” par la centralisation et la coordination de leur activité.
Production
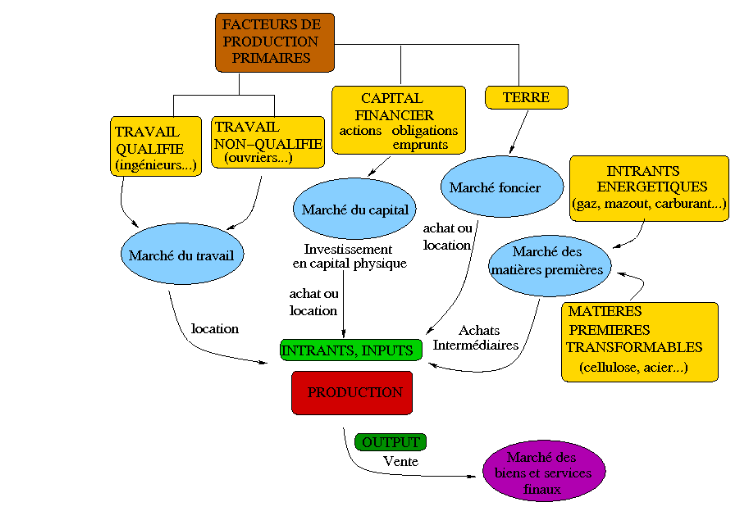Une entreprise transforme des intrants (inputs) en extrants (outputs) via une fonction de production. =⇒ q = f (K, L, T, E, M ) Les facteurs de production: K = capital physique (machines, bâtiments… ); L = travail; E = intrants énergétiques, T = terre, M = matières premières.
- Cette fonction résume les “meilleures” manières (= les plus efficientes) de combiner les facteurs pour produire une quantité donnée du bien/service.
- On peut simplifier avec les deux facteurs de production principaux: q = f (K, L).
Contraintes
Il existe deux types de contraintes pour l’entreprise:
- Les contraintes liées aux prix du marché:
- Le prix du bien produit;
- Le prix unitaire des ressources;
- Les contraintes technologiques de production:
- Limite physique de transformation d’intrants en output en fonction d’une technologie donnée.
- L’entreprise choisit toujours ses ressources en minimisant le coût total.
- Selon l’horizon-temps (court ou long), elle dispose d’une plus ou moins grande flexibilité dans l’ajustement de certains facteurs de production.
Horizon-temps
L’entreprise peut planifier sa production de deux manières:
- À long terme: Horizon “stratégique”, où l’on planifie l’activité future de l’entreprise et sa capacité K (bâtiments, machines, etc).
- À court terme: À l’échelon inférieur, l’entreprise doit prendre des décisions au jour le jour sur la quantité à produire en prenant la capacité comme une donnée fixe (K). Les décisions qui ont été prises dans une optique de long terme sur la capacité sont irréversibles à court terme. Le seul facteur de production pouvant être ajusté à court terme est le travail (L).
Fonction de production à long terme
- L’entreprise souhaite produire une certaine quantité q du bien en utilisant toutes les ressources à disposition qu’elle peut planifier en toute liberté.
- La “capacité” physique (ou capital, abrégé K), en particulier, est déterminée dans cet horizon temporel sans contrainte. L = travail.
- La fonction de production de long terme: q = f (K, L) indique la quantité maximale qui peut être produite en utilisant les facteurs de production de manière efficiente.
Taille et rendements d’échelle
Rendements d’échelle: Que se passe-t-il sur la production si on varie l’échelle de l’entreprise en changeant tous les facteurs de production dans les mêmes proportions (exemple: on double tous les facteurs de production)? Doublons tous les facteurs:
- q0 = f (K0, L0) =⇒ q1 = f (2 × K0, 2 × L0).
On sait que le volume q1 sera plus grand que q0, mais de combien? Double-t-il aussi? Fait-il plus que doubler? Moins que doubler? Selon que:
- q1 = 2 × q0 (changement proportionnel): rendements d’échelle constants;
- q1 > 2 × q0 (changement plus que proportionnel): rendements d’échelle croissants (beaucoup= bien);
- q1 < 2 × q0 (changement moins que proportionnel): rendements d’échelle décroissants. Moins= bien.
Exemple
- Soit la fonction de production à deux facteurs de production (capital et travail): q = f (K, L) = √K × L0.8.
- Choisissons un niveau de capital K0 = 36 avec L0 = 100 travailleurs. On produit q0 = √36 × 1000.8 = 238.9.
- Quadruplons le capital et le travail: K1 = 4 × K0 = 4 × 36 = 144 et le nombre de travailleurs: L1 = 4 × L0 = 4 × 100 = 400. La production va-t-elle (plus/moins que) quadrupler?
- Avec K1 t L1, on produit q1 = √144 × 4000.8 = 1448.2.
- Le volume a plus que quadruplé: 1448.2/238.9 ≃ 6. Les rendements d’échelle sont donc ici croissants.
Fonction de production à court terme
L’entreprise souhaite produire une certaine quantité q du bien en utilisant les ressources à disposition: la “capacité” physique (ou capital) fixe à court-terme (K) et le travail (L): q = f (K, L).
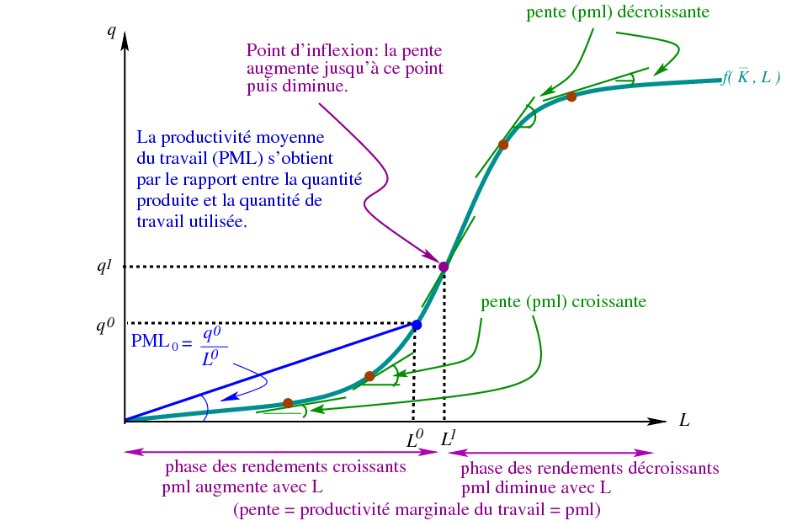
- Cette relation technique entre les facteurs de production et la quantité produite du bien permet de mettre en évidence la notion de productivité moyenne et marginale.
- En multipliant la quantité produite q par le prix du bien, on obtient la recette totale (ou le “revenu” ou le “chiffre d’affaire”).
- Corollaire: en multipliant les productivités physiques par le prix du bien on obtient un rendement moyen ou marginal ou la valeur (en francs) de la productivité.
Productivité moyenne et marginale physiques
- Productivité physique = mesurée en unités du bien:
- La productivité moyenne = “combien d’unités du bien chaque travailleur produit en moyenne”:
- La productivité marginale = “de combien d’unités du bien s’accroît la production avec un travailleur supplémentaire”:
Productivité moyenne et marginale en valeur
Productivité en valeur = “rendement”, “revenu” = mesurée en francs:
- La productivité moyenne en valeur = “combien de francs rapporte en moyenne chaque travailleur”:
- La productivité marginale en valeur= “de combien de francs s’accroît le revenu de l’entreprise avec un travailleur supplémentaire”:
La loi des rendements décroissants
Hypothèse: À court terme, cette relation technique obéit à la loi des rendements décroissants = productivité marginale du travail décroît avec la quantité de travail.
- Intuition : la capacité étant fixe, rajouter des travailleurs ne peut pas accroître la production toujours proportionnellement.
- Exemple: dans un bureau, les travailleurs commencent à se gêner et se relayer sur un ordinateur ou une photocopieuse avec des attentes et des problèmes de coordination.
- NB: Il est possible d’avoir une phase de rendements initialement croissants.
- Généralisation: La loi des rendements décroissants s’applique pour tout facteur de production variable combiné à un facteur de production fixe.
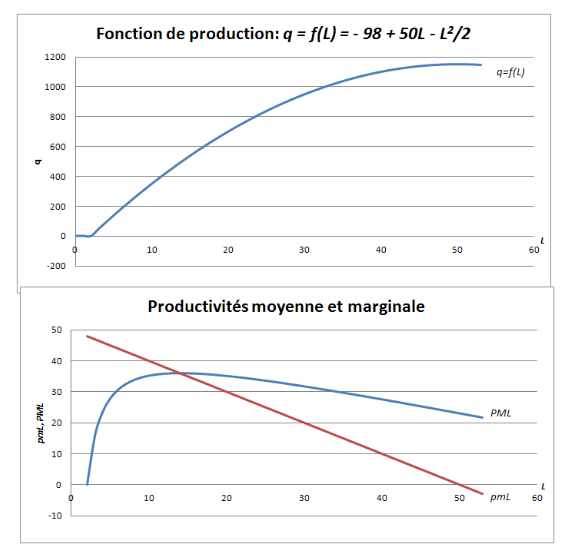
Cas général d’une fonction de production de court-terme
Les coûts de l’entreprise
- À court terme,
- Composante fixe (CF) liée à l’irreversibilité de l’investissement en capacité (ou capital physique).
- Composante variable (CV(q)) associée à la rémunération des travailleurs (la masse salariale) ou autres intrants variables.
- À long terme, la plupart des coûts sont variables, car l’entreprise peut ajuster à souhait sa capacité de production.
- Le coût s’exprime en fonction de la quantité produite, car c’est la variable de choix pour maximiser le profit de l’entreprise.
Les coûts à court terme
- Le coût total peut donc s’exprimer comme: CT (q) = CF + CV (q)
- Pour le coût variable, on lit la fonction de production “à l’envers” (fonction réciproque):
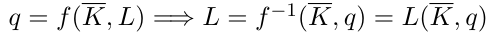
- Lecture: Avec une capacité de court terme donnée par K, L travailleurs sont requis pour produire la quantité q.
- On en déduit la masse salariale correspondante en multipliant ces heures de travail par le taux de salaire horaire (w):
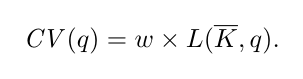
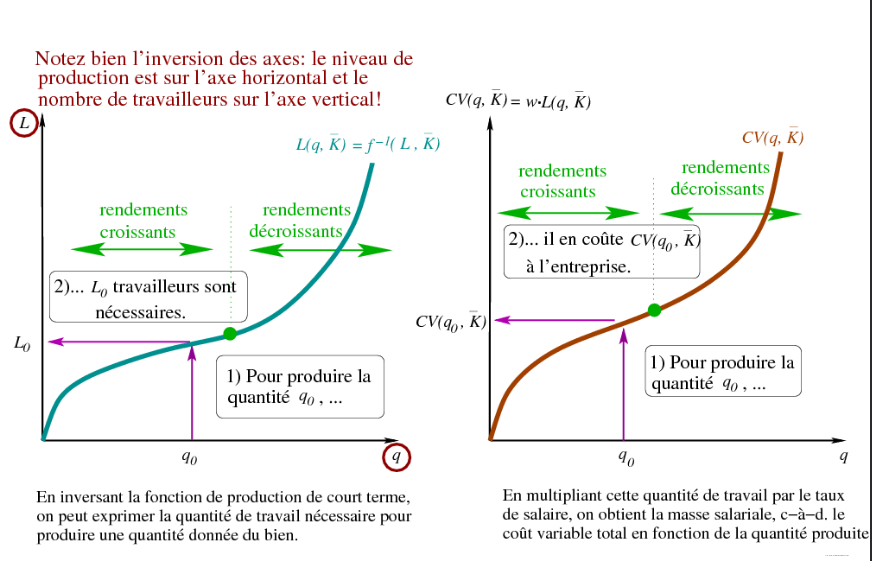Coût total
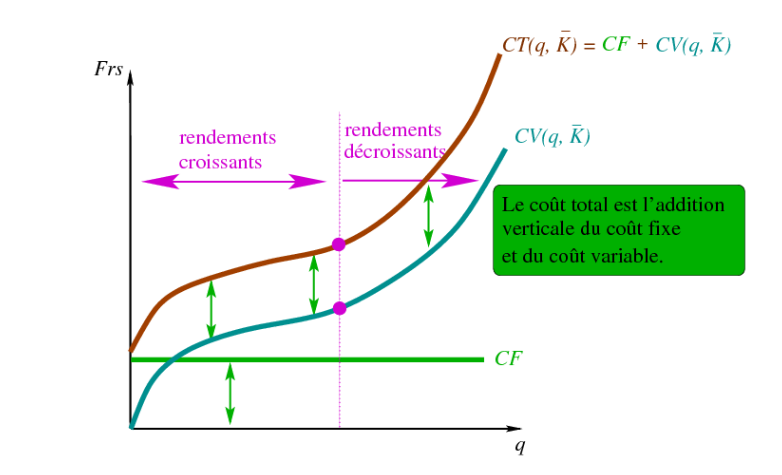CV+Cfixes=CT
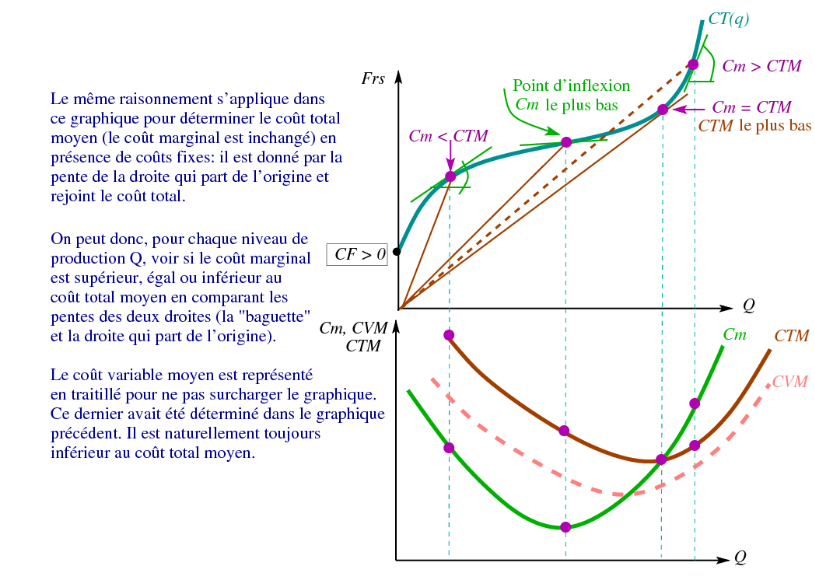
Les coûts moyens
- Le coût fixe moyen est le coût fixe par unité produite:
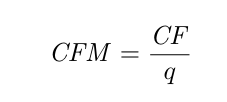
- Le coût variable moyen est le coût variable par unité produite:
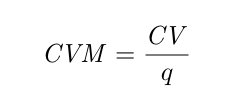
- Le coût total moyen est le coût total par unité produite, soit l’addition du coût fixe moyen et du coût variable moyen:
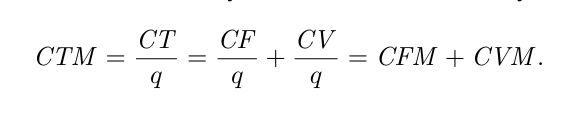
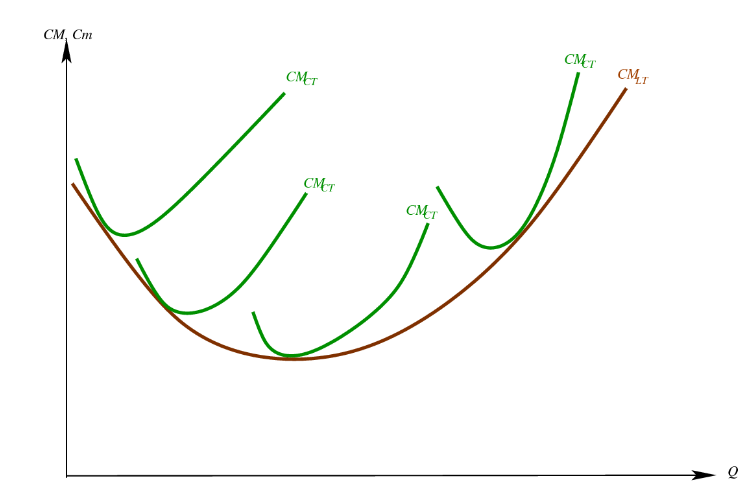
Forme
La courbe de coût total moyen est en forme de U:
- À des niveaux de production très bas, le coût total moyen est élevé parce que le coût fixe est réparti sur un petit nombre d’unités seulement.
- Le coût moyen total diminue avec l’augmentation de la production.
- Le coût moyen total augmente dès lors que le coût variable moyen augmente de façon significative.
- La base de la courbe de coût moyen total (CT M ) en forme de U correspond à la quantité qui minimise le coût moyen total.
- Cette quantité est souvent appelé la taille minimale efficiente de production de la firme.
Le coût marginal
Le coût marginal (Cm) mesure de combien varie le coût total lorsqu’on produit une unité (ou une très petite quantité) supplémentaire:
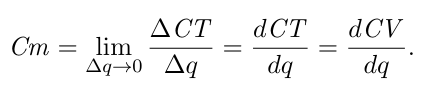Par définition, le CF ne varie pas lorsque la quantité est modifiée, donc le Cm nous indique nécessairement la variation du CV. L’hypothèse des rendements décroissants se vérifie lorsque le coût marginal est croissant.
Le coût marginal intercepte le coût variable moyen à son minimum.
Forme
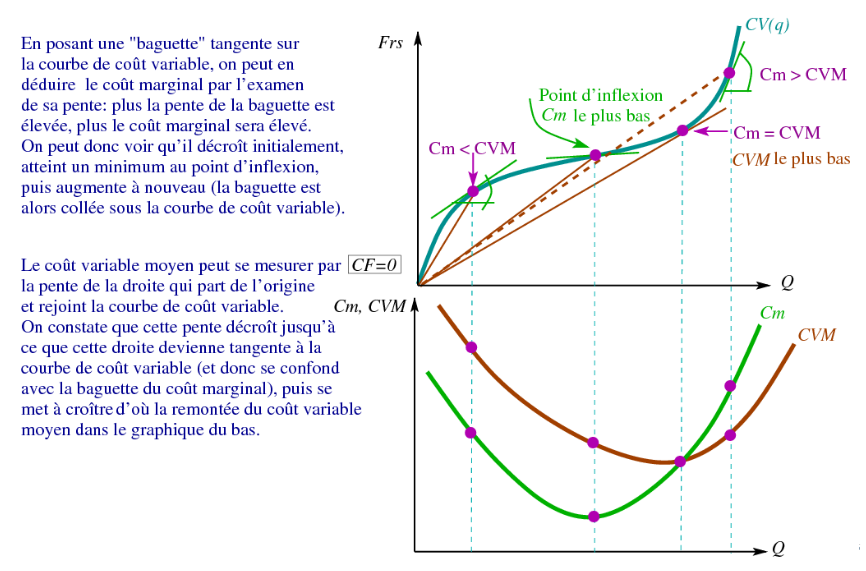
Exemple
Soit une société de consulting & audit qui dispose d’un espace-bureaux de K = 200 m2 loué 10’000.-. Le taux de salaire horaire en vigueur est de w = 100.
- Pour produire q = 10 audits par mois, 12 travailleurs à plein-temps (182 heures/mois: L = 12 × 182) sont nécessaires.
- Le coût total sera de:
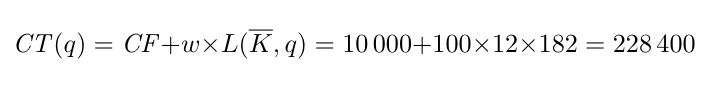
- Pour produire q = 11 audits par mois, 14 travailleurs à plein-temps (182 heures/mois: L = 14 × 182) sont nécessaires.
- Le coût total sera de:
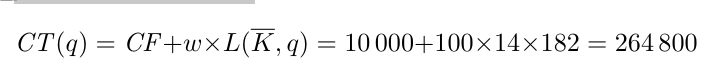
- Coût marginal? Coût moyen? CMar=264 800-228 400. CMoy=264 800/11.
Conclusion
- Lorsque le coût marginal est supérieur au coût moyen, le coût moyen est croissant, alors qu’il est décroissant si le coût marginal lui est inférieur;
- Le coût marginal intersecte le coût total moyen et le coût variable moyen à leur minimum;
- Le coût fixe moyen est nécessairement décroissant.
Économies et déséconomies d’échelle
- Économies d’échelle: propriété selon laquelle le coût moyen total de long terme diminue lorsque la production augmente.
- Déseconomies d’échelle: propriété selon laquelle le coût moyen total de long terme augmente lorsque la production augmente.
- Rendements d’échelle constants: propriété selon laquelle le coût moyen total de long terme ne varie pas lorsque la production augmente.
