Intervalles de confiance pour une moyenne, test-z et test-t
Niveau de signification


Exemple : âge des véhicules
- Dans une enquête menée auprès de 30 adultes, l’âge moyen du véhicule principal d’une personne est de 5.6 ans.
- En supposant que l’écart-type de la population est de 0.8 an.
- Trouvez la meilleure estimation ponctuelle de la moyenne de la population et un intervalle de confiance à 90% pour cette moyenne.

Étapes pour calculer un intervalle de confiance pour µ avec σ connu

Marge d’erreur et taille d’échantillon

Exemple : quelle est la taille de l’échantillon
- Le président d’une université demande au professeur de statistiques d’estimer l’âge moyen des étudiants de l’université.
- En supposant que l’écart-type de la population est de 3 ans, quelle taille d’échantillon est nécessaire pour obtenir un intervalle de confiance à 99% pour l’âge moyen des étudiants avec une marge d’erreur E = 1 ?

Intervalle de confiance pour la moyenne µ de la population avec σ inconnue
- Taille de l’échantillon grande (n > 30), population IID.
- Taille de l’échantillon petite (n < 30), population IID normale.
Grande taille d’échantillon, population IID

Petite taille d’échantillon, population IID normale
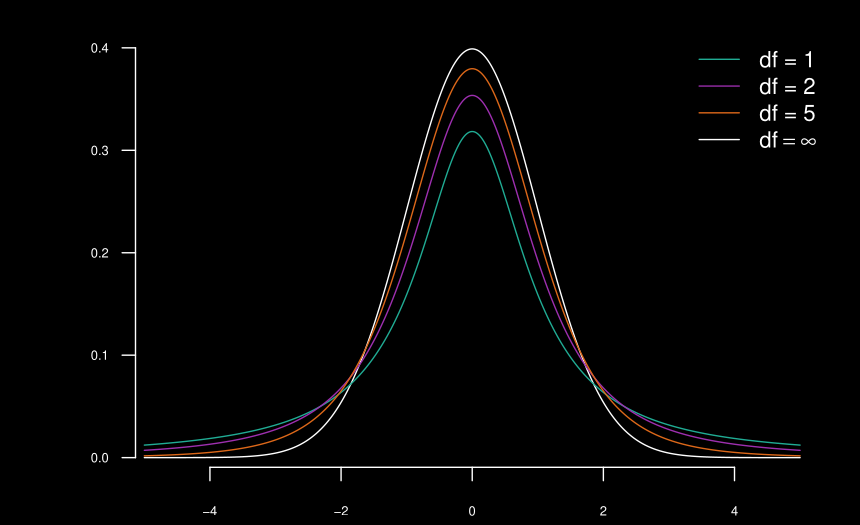

Exemple : âge des véhicules

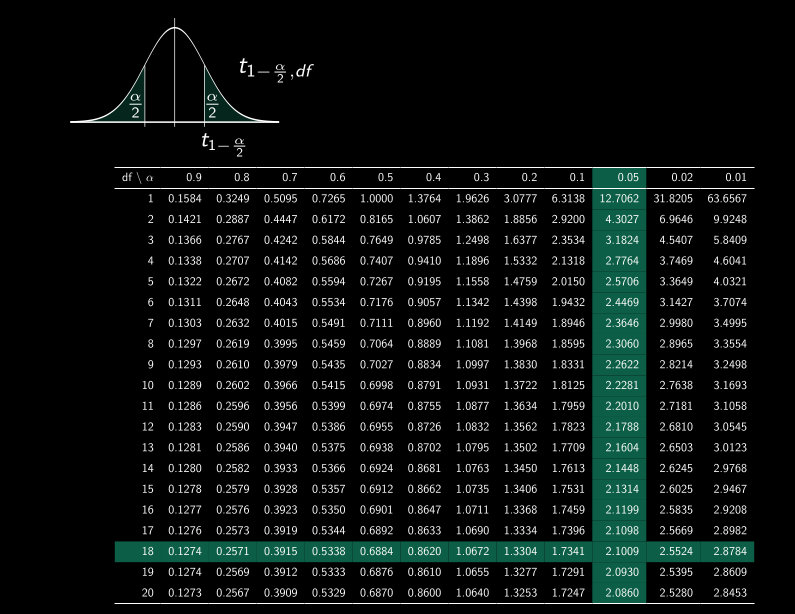

Étapes pour calculer un intervalle de confiance pour µ avec σ inconnu et n ≤ 30

Test d’hypothèse
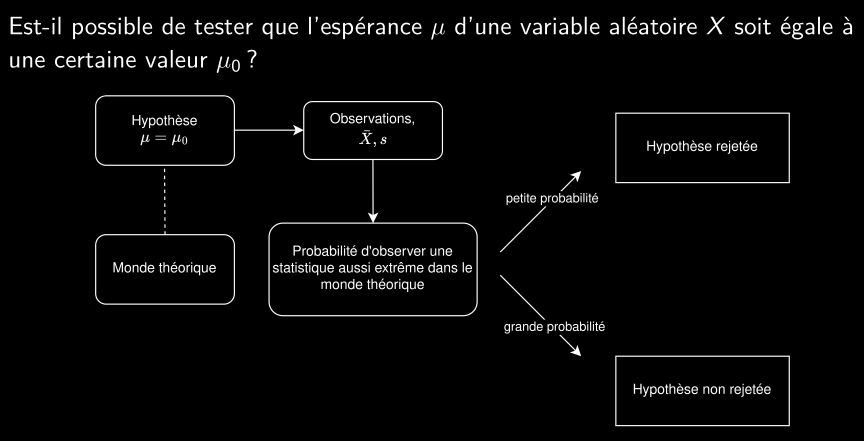
Hypothèse nulle et alternative


Exemple : tester sur la taille des étudiants

Exemple : tester un nouveau régime

Statistique de test
- Un test de signification est basé sur une statistique de test qui montre si les données fournissent ou non des preuves contre l’hypothèse nulle.
- Quand H0 est vrai, on s’attend à ce que l’estimation prenne une valeur proche de celle spécifiée par H0.
- Des valeurs de l’estimation éloignées de celle spécifiée par H0 fournissent des preuves contre H0 . L’hypothèse alternative détermine dans quelle(s) direction(s) comptent les écarts contre H0.
Statistique de test pour la moyenne de la population


P-valeur

Décision
Exemple→Test-Z : taille moyenne différente de 1.75m?

Exemple→Test-Z : le régime fait-il perdre du poids

Graphique de la p-valeur
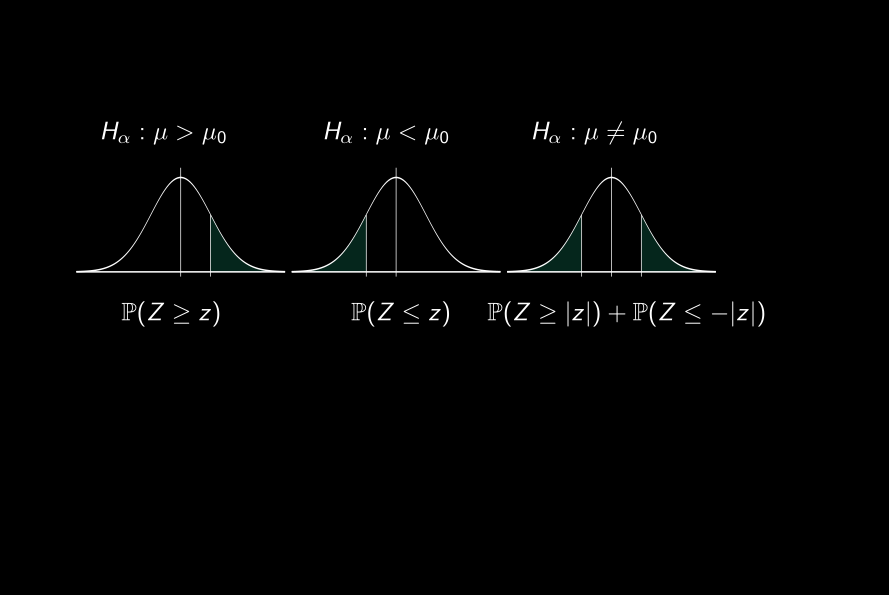
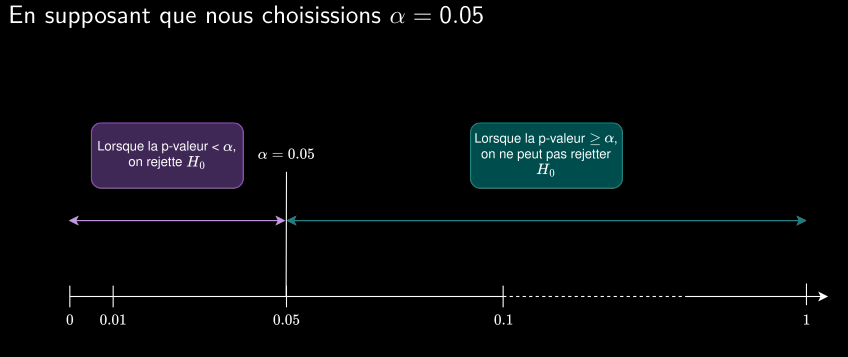
P-valeur
- La p-valeur est la probabilité, en supposant que H0 soit vrai, que la statistique de test prenne une valeur au moins aussi extrême que celle effectivement observée.
- Plus la p-valeur est petite, plus les preuves contre H0 fournies par les données sont fortes.
- Si α=0.05, nous exigeons que les données fournissent des preuves suffisamment solides contre l’hypothèse nulle pour que son rejet se produise au maximum 5 % du temps lorsque H0 est vrai.
Statistique de test pour la moyenne de la population

Décision basée sur la valeur critique

Exemple : test-t
- On considère l’âge des étudiants inscrits au bachelor en relations internationales.
- On considère que la distribution de l’aĝe des étudiants est distribuée normalement.
- On considère un échantillon de 20 étudiants pour lequel on mesure leur âge.
- La moyenne de l’échantillon est de X̄ = 21.42 et l’erreur standard de l’échantillon est de s = 2.91.
- Vous chercher à tester si l’âge moyen des étudiants est supérieur à 18 ans à un niveau de significativé de α = 0.05.
- Les hypothèses sont donc :
- H0 : µ = 18.
- Hα : µ > 18.

Étapes pour effectuer un test d’hypothèse
- Étape 1 : Formuler l’hypothèse nulle (H0 ) et l’hypothèse alternative (Hα ).
- Étape 2 : Calculer la valeur de la statistique de test zobs ou tobs.
- Étape 3 : Comparer la statistique de test à la valeur critique ou trouver la p-valeur pour les données observées et comparer la p-valeur avec le niveau de signification désiré α.
Variance
