Inférence statistique
Incertitude et prise de décision
- Dans notre exemple, nous souhaitons savoir si p, une quantité au niveau de la population, est supérieure ou inférieure à 50%.
- Malheureusement, p est généralement inconnu car nous ne pouvons pas accéder à l’ensemble de la population. Nous utilisons donc p̂ à la place, une quantité dépendante de l’échantillon.
- Cependant, comme nous pouvons le voir, p̂ est aléatoire puisque c’est une fonction de l’échantillon collecté.
- Pour résoudre ce problème, nous devons évaluer l’incertitude de p̂ (c’est-à-dire évaluer à quel point p̂ et p peuvent être différents).
- Les statistiques nous fournissent de nombreux outils permettant de déterminer l’incertitude ainsi que les risques associés à la prise de décision.
Mesurer l’incertitude?
- L’incertitude peut être mesurée de nombreuses façons différentes. Une approche courante consiste à utiliser des intervalles de confiance, qui reposent sur le théorème central limite (TCL) qui stipule : La distribution d’échantillonnage de la moyenne d’échantillon se rapproche d’une distribution normale à mesure que la taille de l’échantillon augmente.
- En termes simples, nous pouvons traduire le TCL par :

Distribution asymptotique de p̂
Dans le cas d’une proportion, la moyenne de l’échantillon est dénotée par p̂ et par le TCL, la distribution de l’estimateur tend vers :
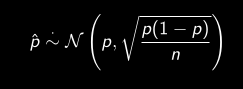
Intervalles de confiances



Décisions et précision en statistiques
- Étant donné que les données sont disponibles par échantillonnage, elles sont aléatoires. Par conséquent, une décision ou une prédiction ne peut jamais être faite avec certitude !
- La seule certitude que l’on peut avoir est, par exemple, qu’une proportion sera toujours incluse dans l’intervalle de 0 % à 100 %. Cependant, cela n’est ni informatif ni utile et ne dépend même pas des données.
- Il existe un compromis entre le risque, mesuré par 1 − α (généralement 95 %), le niveau de confiance, et la précision de la conclusion, mesurée par exemple par la longueur de l’intervalle de confiance.
- Plus la taille de l’échantillon est grande, plus la conclusion est précise, pour le même niveau de confiance.
- Par conséquent, toute décision basée sur des méthodes statistiques comporte un risque, et la quantité de risque acceptable dépend du contexte.
Comment tester une hypothèse scientifique?
- Une autre mesure résumée de l’incertitude est fournie par les p-valeurs, qui prennent des valeurs entre 0 % et 100 %. Les p-valeurs sont généralement préférées aux intervalles de confiance lorsque nous voulons évaluer la validité d’une affirmation.
- Cependant, les p-valeurs ont souvent été mal utilisées car comprendre ce qu’elles signifient n’est pas intuitif.
- Une p-valeur est associée à une paire d’hypothèses concernant le phénomène étudié. Par exemple, pour l’élection présidentielle américaine, une hypothèse est que la majorité vote pour l’équipe de Biden, et l’autre est qu’il n’y a pas de majorité.
- Chaque hypothèse exclut l’autre, permettant d’exclure l’une en faveur de l’autre à l’aide des données.
- L’hypothèse nulle est celle que l’on ne pourra jamais prouver car les données sont aléatoires.
- L’hypothèse alternative est celle qui offre plus de choix de valeurs et a donc une chance d’être favorisée par rapport à l’hypothèse nulle (par exemple, l’équipe de Biden reçoit plus de 50 % des votes).
Test d’hypothèse
- Informellement, une p-valeur peut être comprise comme une mesure de la plausibilité de l’hypothèse nulle étant donné les données. Plus la p-valeur est petite, plus l’incompatibilité de l’hypothèse nulle avec les données est grande.
- Lorsque la p-valeur est suffisamment petite (généralement inférieure à 5 %), on dit que le test basé sur les hypothèses nulles et alternatives est significatif ou que l’hypothèse nulle est rejetée en faveur de l’hypothèse alternative.
- Lorsque la p-valeur n’est pas suffisamment petite (généralement supérieure à 5 %), avec les données disponibles, nous ne pouvons pas rejeter l’hypothèse nulle et alors rien ne peut être conclu.
- Avec un échantillon de données, la p-valeur obtenue résume d’une certaine manière l’incompatibilité entre les données et le modèle construit sous l’ensemble des hypothèses.
- La p-valeur (de l’échantillon) est habituellement comparée à une valeur seuil qui fixe le niveau de risque (subjectif) de décision en faveur de l’incompatibilité.
- Le niveau de risque est appelé niveau de signification et est une petite valeur, généralement 5 %, mais cela dépend du contexte.
Ce qu’il faut retenir sur les p valeurs
- Une p-valeur est une variable aléatoire, car sa valeur dépend des données. De même, les intervalles de confiance sont aléatoires, car leurs bornes dépendent des données.
- La p-valeur est étroitement liée à la largeur de l’intervalle de confiance correspondant. Plus l’intervalle de confiance est étroit, plus il est probable que la vraie valeur ne soit pas incluse dans l’intervalle, et donc plus la p-valeur est petite.
- Il peut donc arriver que, bien que l’hypothèse nulle ne puisse pas être rejetée (en supposant qu’elle soit vraie), la p-valeur soit inférieure au seuil fixé. Si ce dernier est choisi à 5 %, alors, en moyenne, la p-valeur (de l’échantillon) est inférieure à 5 % une fois sur vingt !
- Par conséquent, effectuer plusieurs tests, avec les mêmes données ou des données différentes, est dangereux car cela conduit automatiquement à des résultats significatifs, alors qu’en réalité il n’y en a pas !
- Les intervalles de confiance et les p-valeurs peuvent être utilisés pour de nombreux types de modèles. Par conséquent, ils peuvent être utilisés pour évaluer la validité de la plupart des hypothèses.
Calcul
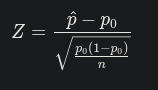

Exemple
