Estimateurs
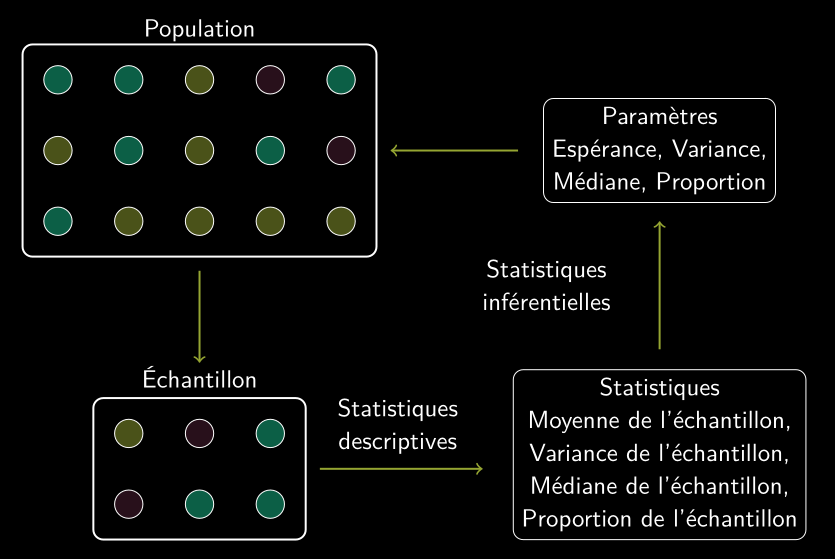
Statistiques descriptives et inférentielles
- Statistiques descriptives : décrire les données que nous avons collectées qui composent l’échantillon.
- Inférence statistique : faire des généralisations sur un ensemble plus large, la population.
Exemple
- Supposons que Stephen Curry ait marqué en moyenne 30.1 points lors de 79 matches de basketball.
- Qu’est-ce qui est aléatoire ?
- Qu’est-ce qui est inconnu ?
- X = points marqués dans un seul match
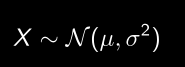
- Qu’est-ce que µ ? Et σ ?
Statistiques vs. paramètres
- Paramètre : une caractéristique de la population. Typiquement inconnue en raison du grand nombre d’individus dans la population et/ou de l’impossibilité de mesurer tous les résultats possibles.
- Statistique : une quantité qui est calculée à partir des données que nous avons collectées de la population (échantillon).

Distribution d’échantillonnage
- Les données sont des variables aléatoires.
- Les statistiques sont des fonctions des données. Elles sont donc aussi des variables aléatoires.
- La distribution des statistiques dépend des paramètres de la distribution des données.
Exemple : Moyenne de l’échantillon

X̄ en tant que variable aléatoire

Espérance
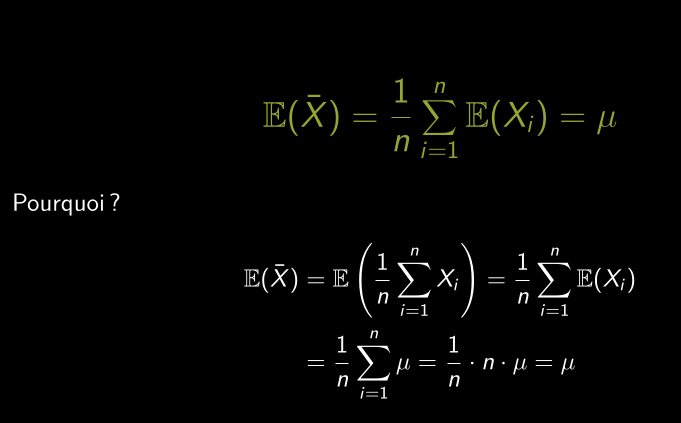
Écart-type

Erreur standard de X̄

Exemple : observations normales et indépendantes

Distribution

Standardisation
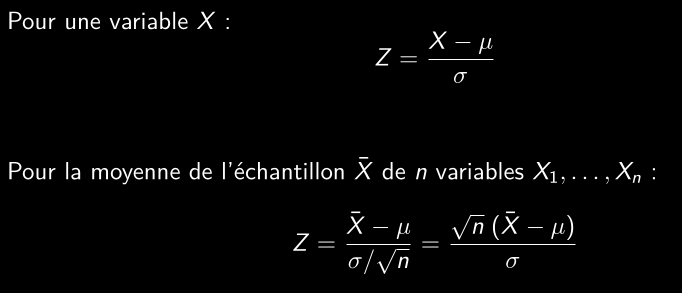
Exemple : Nombre moyen de voitures dans les foyers américains

Échantillon
- Jeu de données de l’échantillon : {X1 , … , Xn }.
- Taille de l’échantillon : n.
- Ordre de l’échantillon : n ≪ N (c’est-à-dire, n est (généralement) grand mais beaucoup plus petit que N).
Objectif
- À partir des valeurs de l’échantillon, {X1 , … , Xn }, où n est la taille de l’échantillon, nous essayons de tirer des conclusions sur les paramètres d’intérêt.
- L’échantillon idéal doit être représentatif et non biaisé.
- Choisir l’échantillon de manière aléatoire.
Échantillon aléatoire simple
{X1 , … , Xn } est un échantillon aléatoire simple si :
- Un membre particulier de la population est choisi, cela n’affecte pas les chances qu’un autre membre soit choisi.
- Chaque membre de la population a la même probabilité d’être choisi.
En d’autres termes…
- {X1 , … , Xn } sont indépendants.
- {X1 , … , Xn } sont identiquement distribués (c’est-à-dire qu’ils ont la même fonction de masse ou fonction de densité de probabilité).
Estimation

Propriétés

Espérance et écart-type

Remarque

Théorème central limite (TCL)

Quand l’utiliser?


Proportion d’échantillon

Distribution d’échantillonage

Laissez n augmenter : n=10⇒100, p=0.5
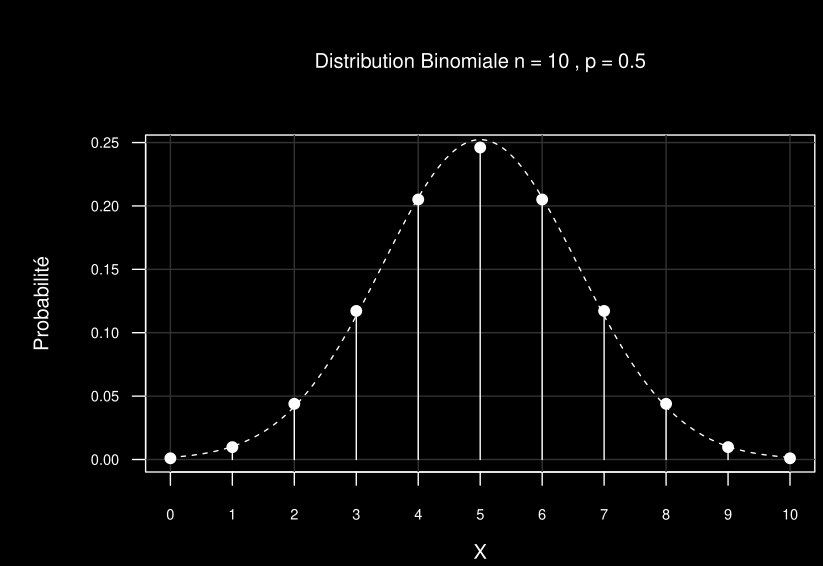
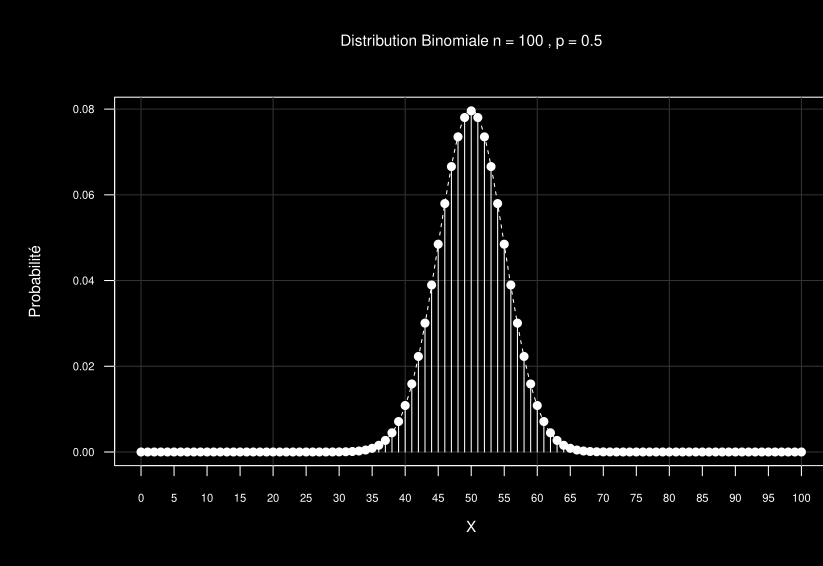
TCL

Quand l’utiliser
