Statistiques descriptives et inférentielles
Définitions
Descriptives
Décrire les données que nous avons collectées qui composent l’échantillon.
Inférence statistique
Faire des généralisations sur un ensemble plus large, la population.
Description des échantillons
- Quelle est sa tendance centrale ?
- Quelle est sa dispersion ou variabilité ? Combien de bruit contient les données ?
- Quelle est la forme de la distribution ? Est-elle symétrique ?
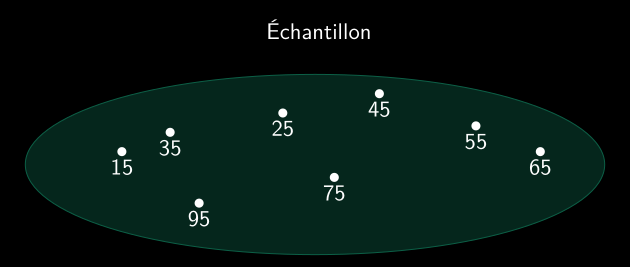
Tendance centrale de la distribution
Mesures de la tendance centrale de la distribution.
Moyenne
Additionner les données et diviser par le nombre d’observations.
Exemples
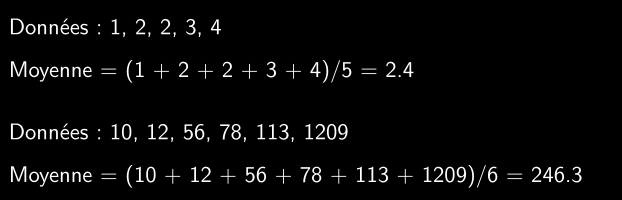
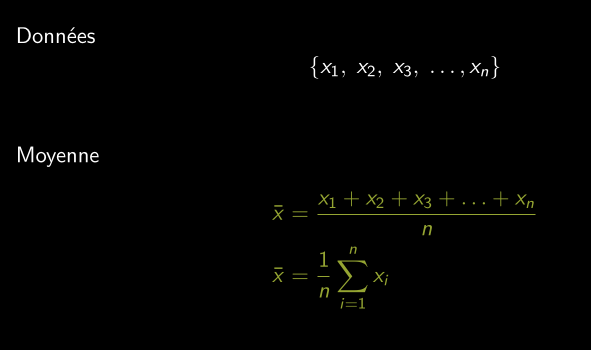
Médiane
Un nombre égal d’observations plus grandes et plus petites que la médiane. Trier les données et considérer la valeur de l’observation centrale.
Exemples
Moyenne versus médiane
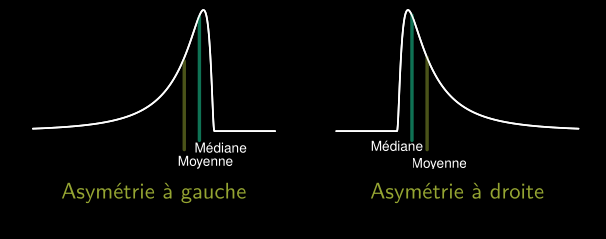
La moyenne et la médiane sont proches pour des distributions symétriques :
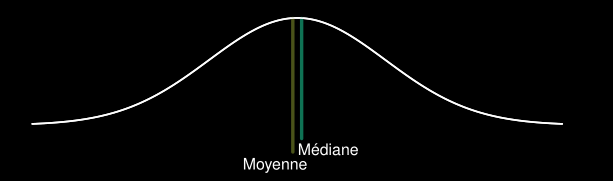La moyenne se déplace dans la direction de l’asymétrie d’une distribution :
Valeurs aberrantes
Une valeur qui ne correspond pas au reste.
Exemples
La médiane est résistante aux valeurs aberrantes!
Résumé en 5 nombres
- Médiane.
- Minimum, Maximum.
- Quartiles : observation centrale au-dessus et en dessous de la médiane.
Trouver les quartiles
- Données : 7, 23, 75, 82, 34, 91, 10.
- Trier, on obtient 7, 10, 23, 34, 75, 82, 91.
- Trouver la médiane, on obtient 34.
- Observations en dessous de la médiane : 7, 10, 23.
- Premier quartile Q1 = 10.
- Observations au-dessus de la médiane : 75, 82, 91.
- Troisième quartile Q3 = 82.
Autre exemple
- Données : 7, 8, 22, 38, 48, 62.
- Médiane = (22+38)/2 = 30.
- Premier Quartile : 7, 8, 22.
- Q1 = 8.
- Troisième Quartile : 38, 48, 62.
- Q3 = 48.
Mesurer la dispersion
Quelle est la variabilité des données?
- Étendue = Maximum-Minimum.
- Étendue Interquartile (IQR) : Q3-Q1.
- Écart-Type (s) : Racine carrée de la moyenne des distances quadratiques à la moyenne.
Écart-type de l’échantillon
5 étapes faciles
- Calculer la moyenne x̄.
- L’élever au carré.
- Calculer la somme des x².
- Trouver la différence (somme des xi² ) − nx̄².
- Diviser par n − 1.
- Prendre la racine carrée.
Exemple : 7, 8, 3
IQR versus s
- L’IQR, comme la médiane, ne dépend pas des observations les plus grandes (ou les plus petites).
- L’IQR est résistant aux valeurs aberrantes.
- s dépend de toutes les données et peut être sensible aux observations éloignées (valeurs aberrantes).
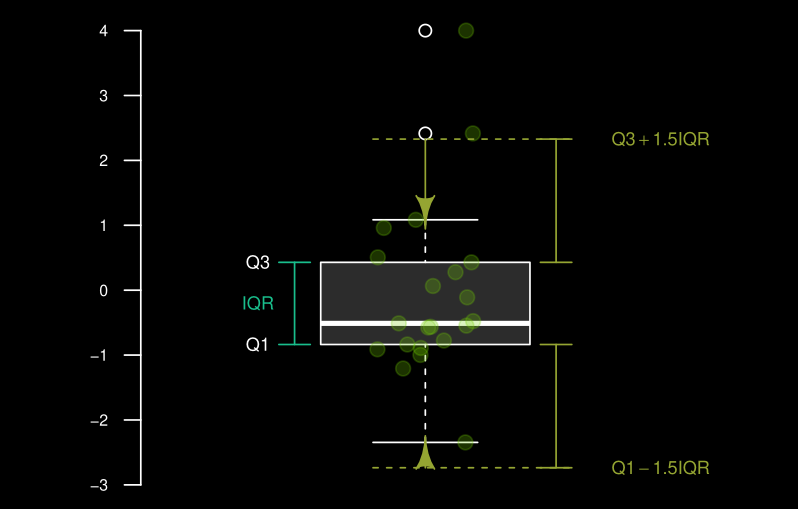
Les aberrantes apparaissent en dessous du Q1 et en haut du Q3 après une distance de 1.5 X IQR.
Variables
Variables
L’aspect qui diffère d’un sujet à un autre, d’un individu à un autre, par exemple l’orientation politique, l’âge, le sexe, le revenu, etc.
Données
La valeur des variables, par exemple : Conservateur, 19, Homme, 15 000$, etc.
Deux types de variables
Il y a quatre sous-types.
Quantitatives ou numériques
Nombres, mesures : âge, taille, distance parcourue, heures de sommeil, revenu, etc.
Continues vs discrètes
Catégorielles
Classifier chaque observation : nationalité, langue maternelle, satisfaction du cours, niveau d’études, etc.
Nominales versus ordinales
Boxplot
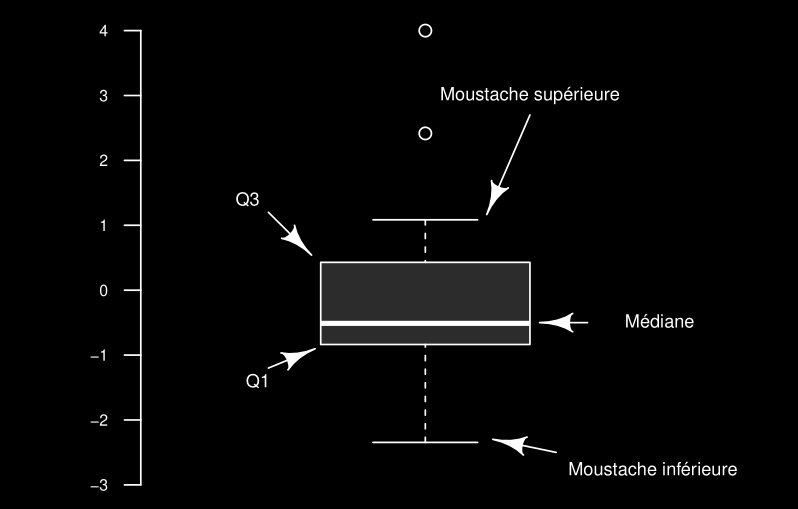
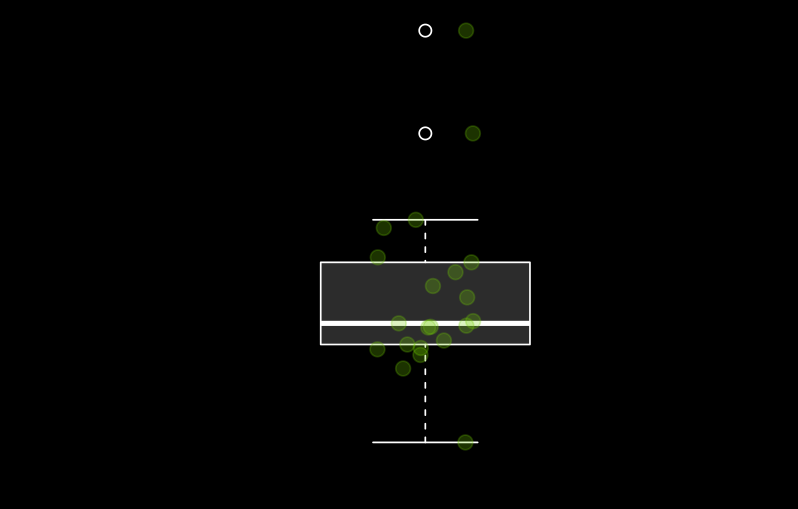Chaque point est une observation réelle.
Comparaison entre groupes
Boxplot côte à côte pour comparer deux ensembles de données ou plus :
- Ont-ils le même centre ? La même forme ? La même dispersion ?
- La différence entre les médianes est-elle beaucoup plus grande que la variabilité des données ?
Exemple : résultats de tests pulmonaires avant et après traitement
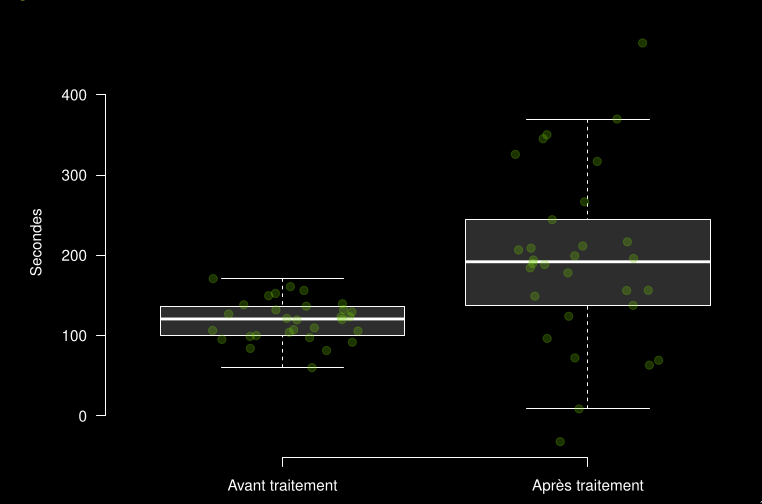
L’histogramme
Exemple : heures de sommeil
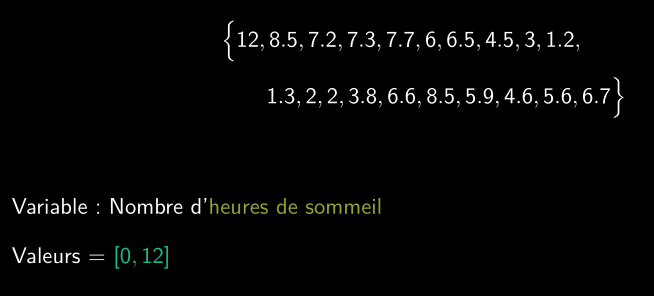
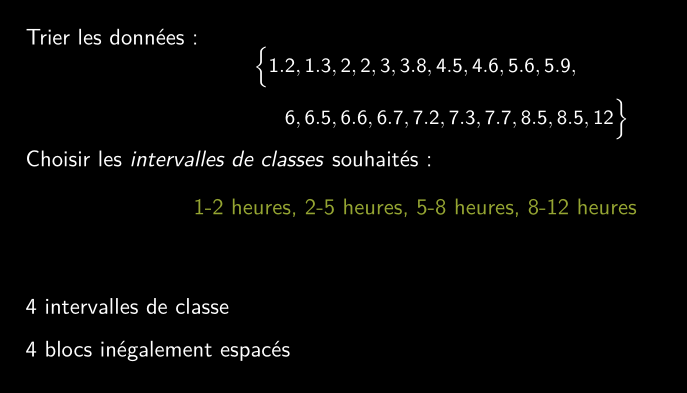
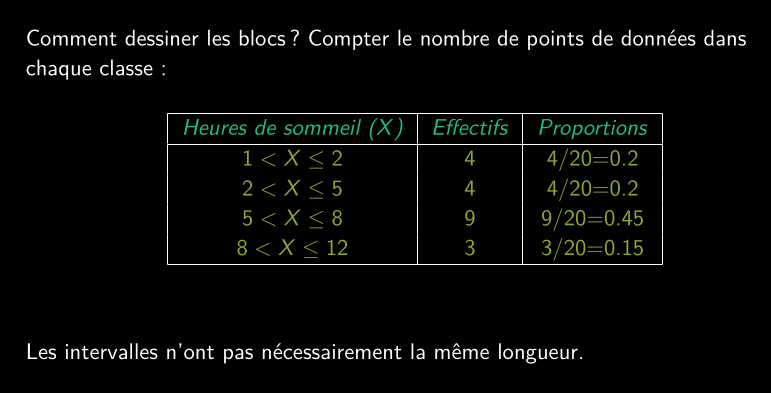
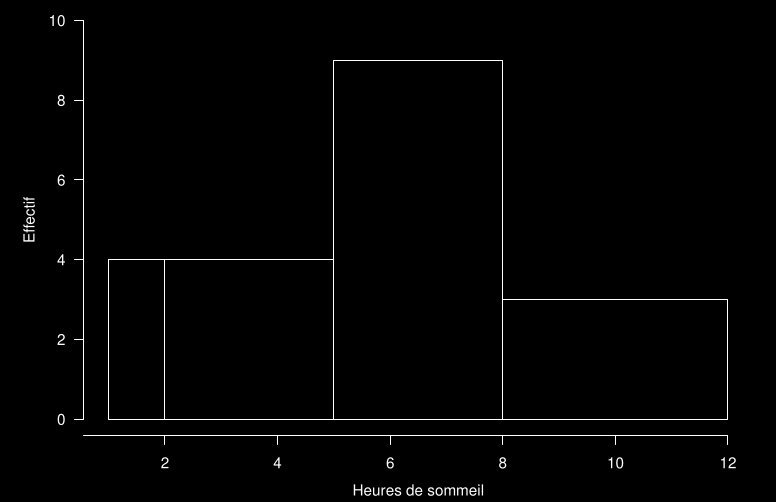
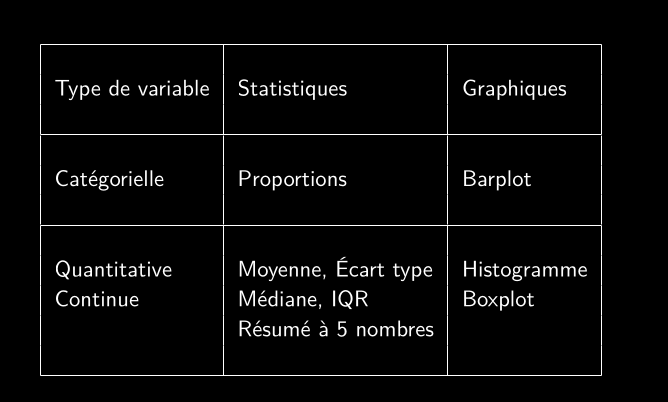
Visualiser les données catégorielles
- Donner une image claire de ce que contiennent les données.
- Souligner les différences/similitudes.
- Les barplot sont généralement les meilleurs.
Donc
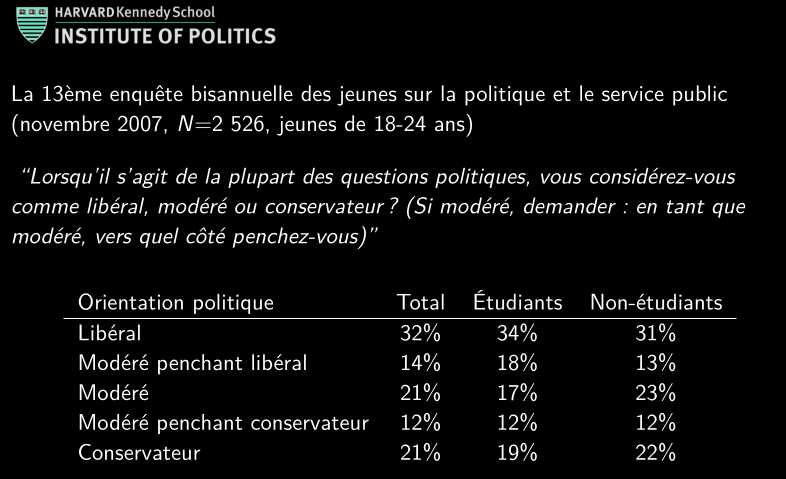
Barplot→ Exemple : orientation politique
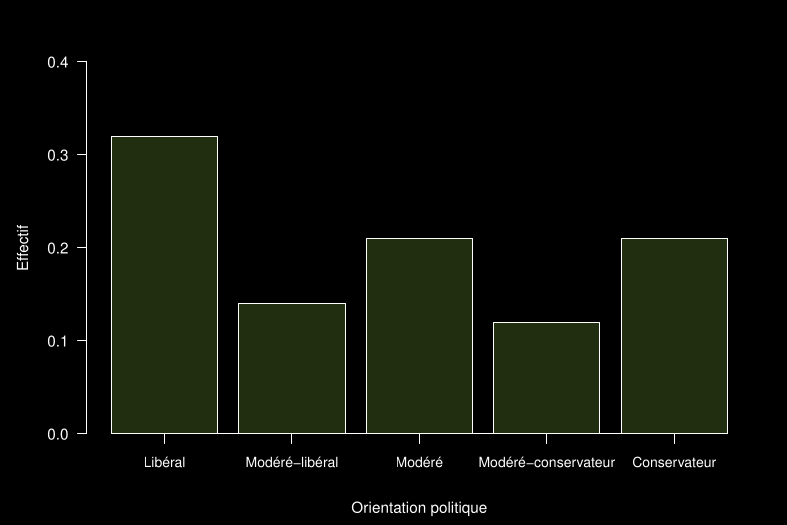
Loi uniforme
Loi normale
