Motivation
La distribution normale, ou gaussienne, est l’une des distributions les plus importantes en statistique.
Elle apparaît naturellement dans de nombreux phénomènes physiques, biologiques et sociaux.
Théorème central limite : La somme/moyenne de variables aléatoires indépendantes tend vers une distribution normale, même si les variables initiales ne suivent pas une distribution normale.
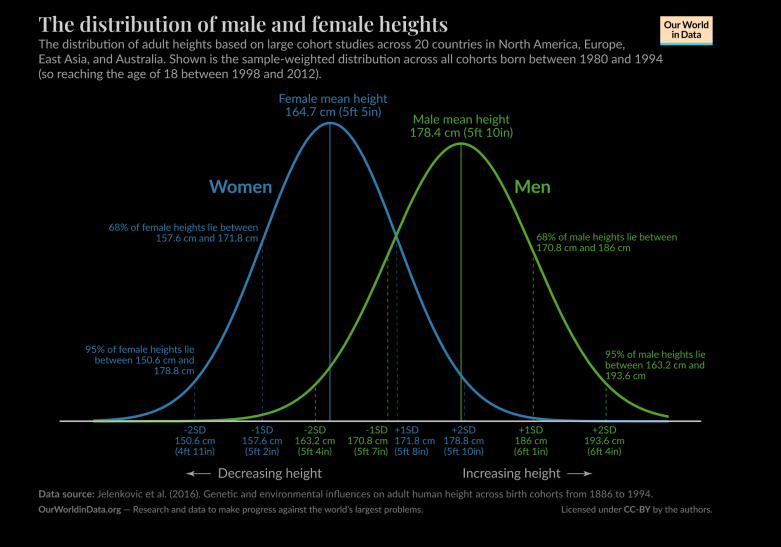
La hauteur des femmes en cm (dénotée X ) est distribuée normalement avec une
espérance de 164.7 cm et un écart type de 7.1 cm:
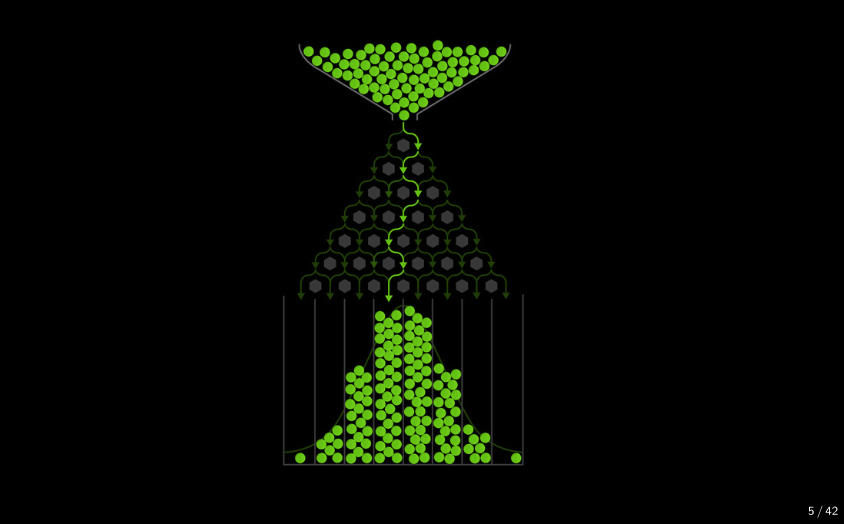
La planche de Galton
La planche de Galton est un dispositif qui illustre comment des événements aléatoires peuvent conduire à une distribution normale.
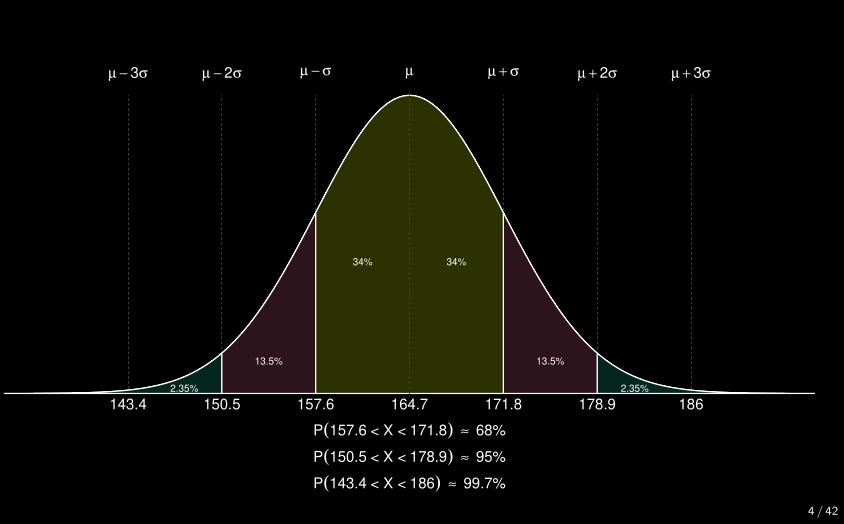
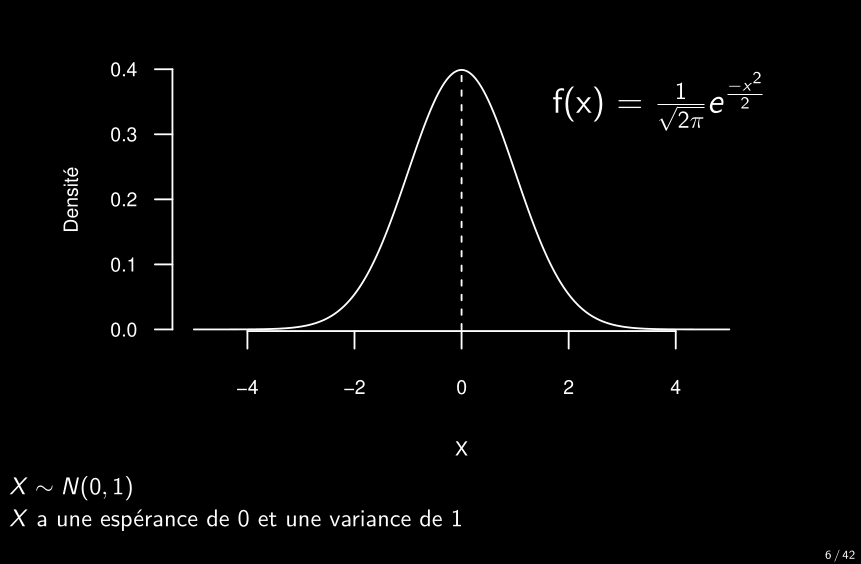
Densité de la distribution standard normale
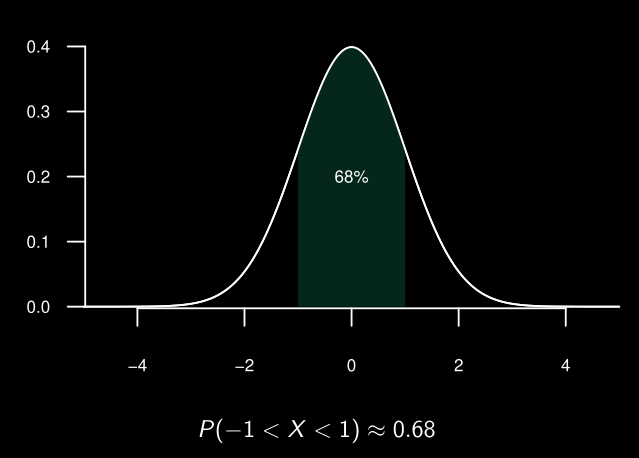
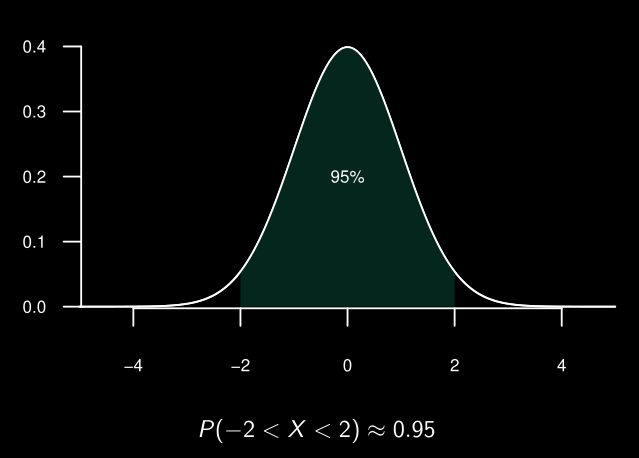
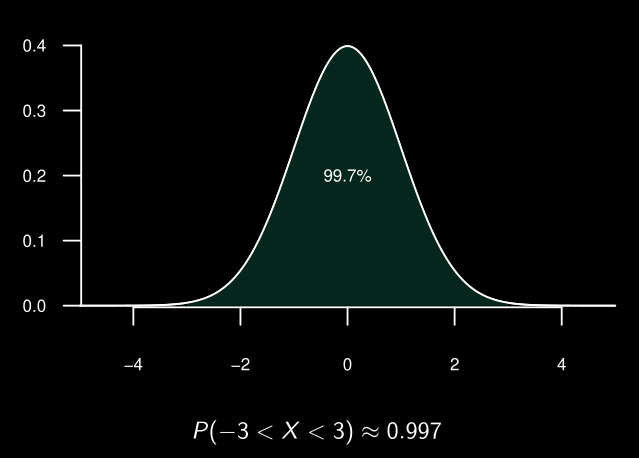
La fonction de distribution cumulative
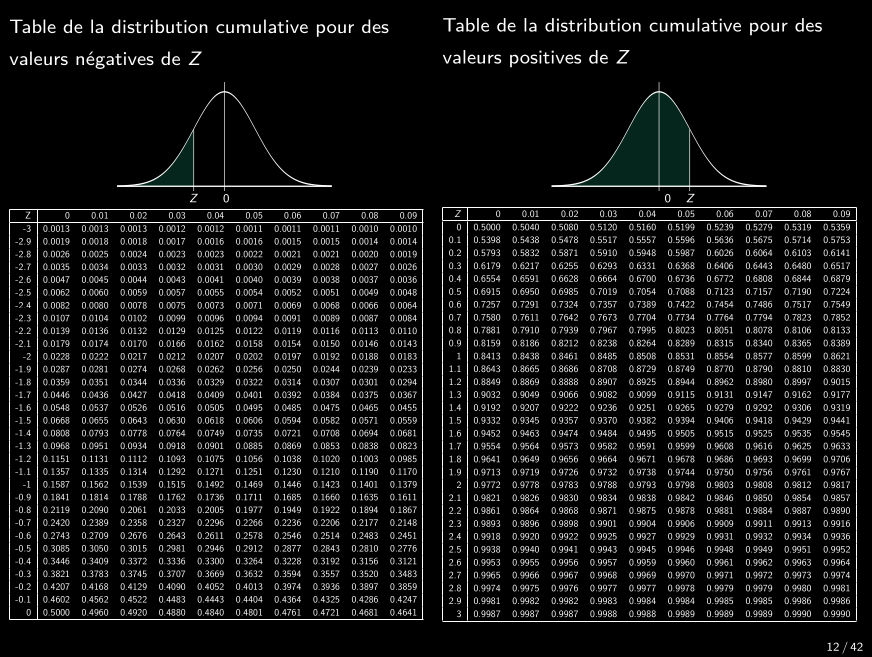
Calcul
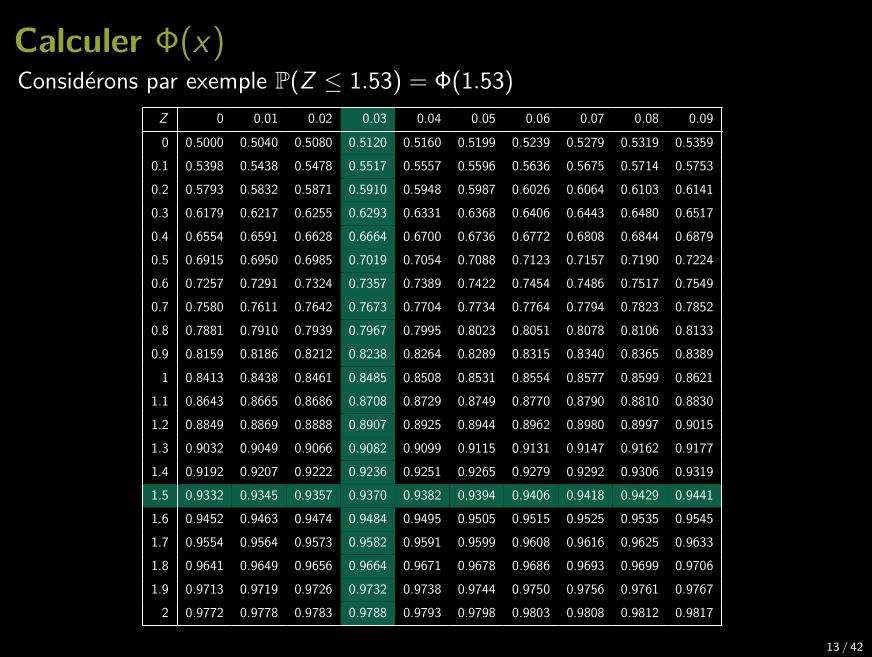
Calcul du complément
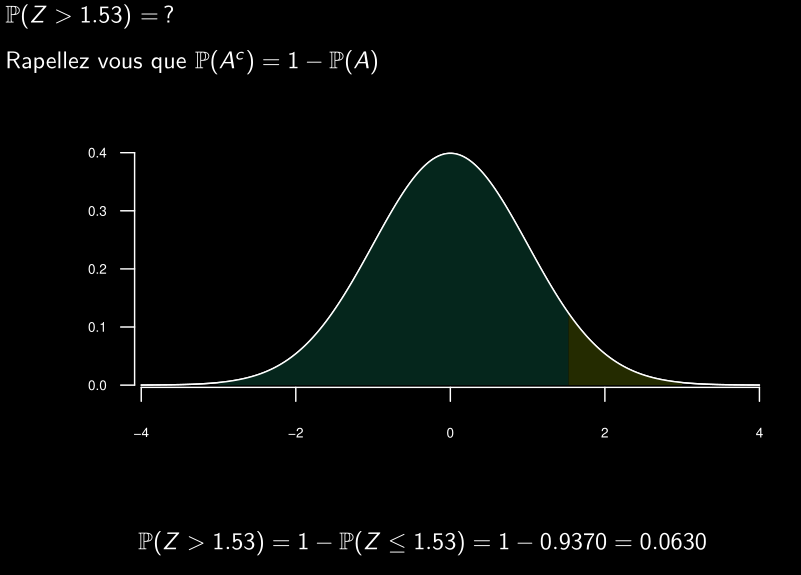
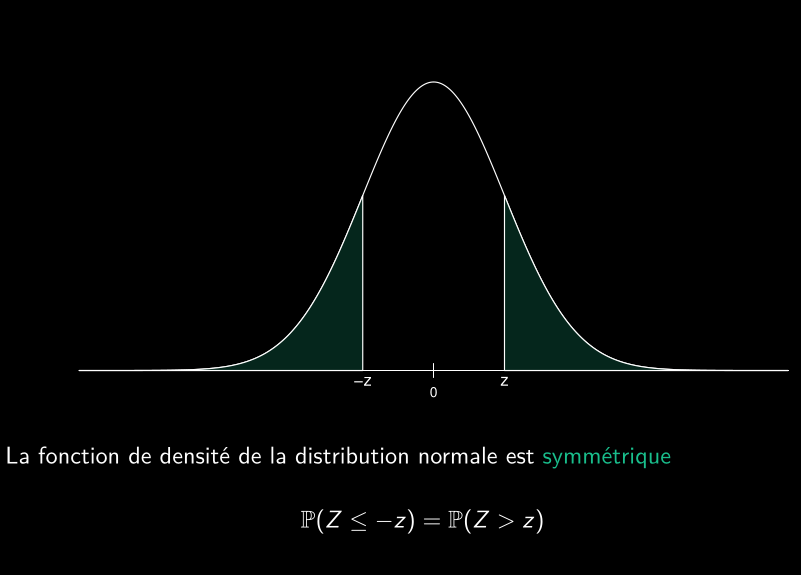
Symmétrie de la distribution normale
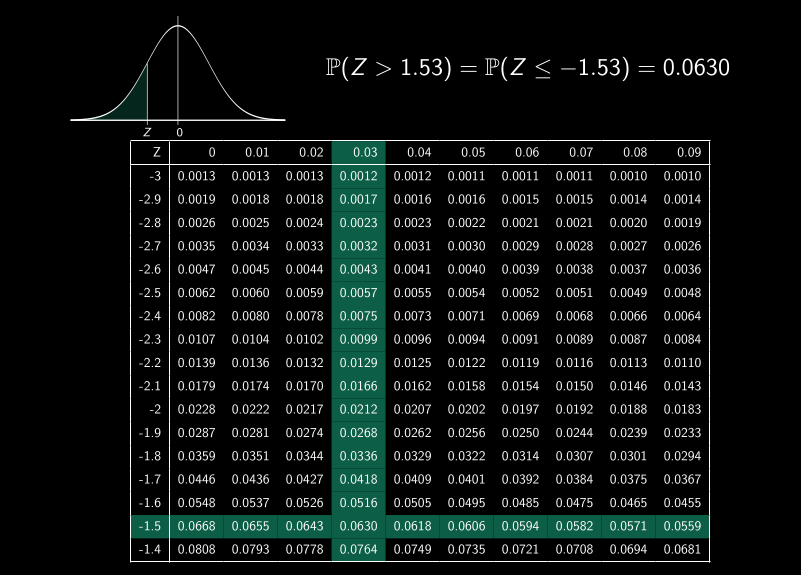
Calcul de probabilité d’intervalles
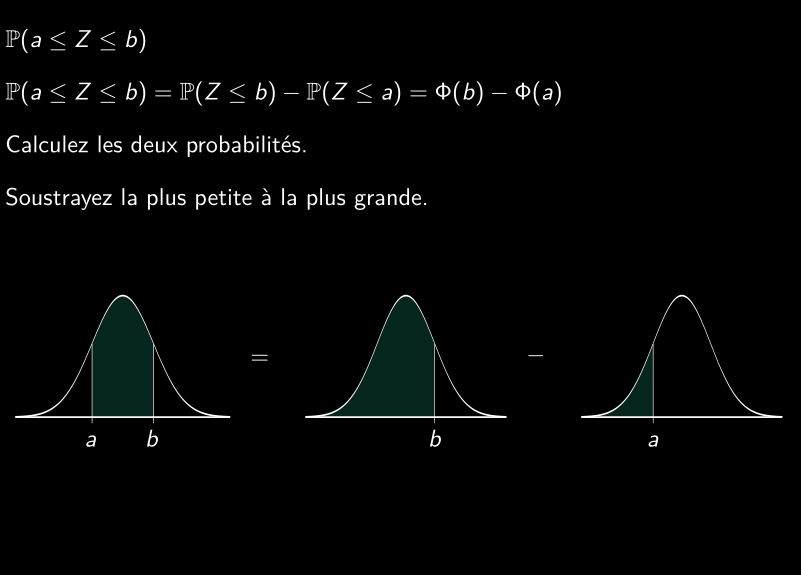
Valeur non présentes dans la table
Distribution Normale
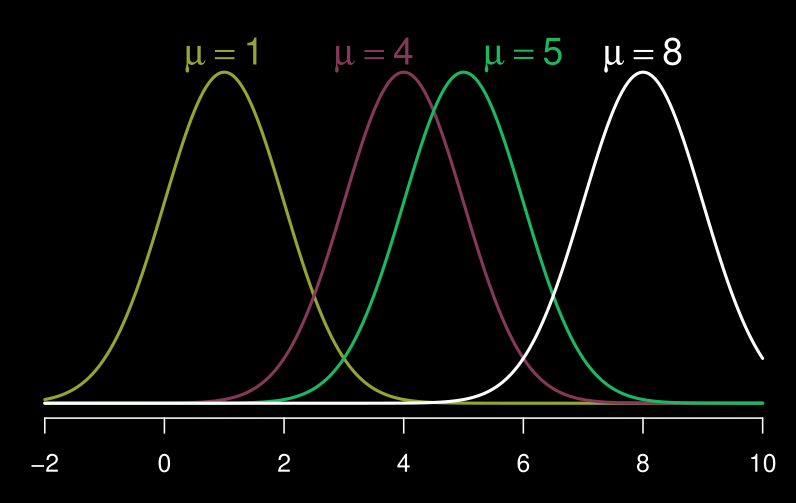
Différentes moyennes
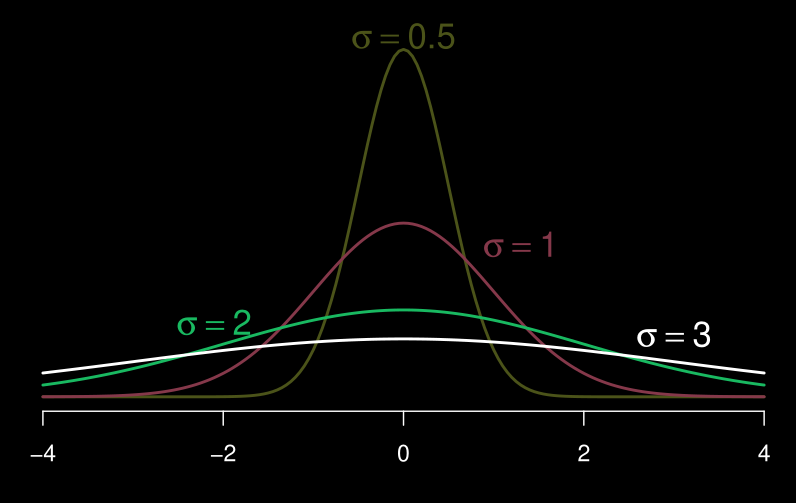
Différents écarts-types
Comment calculer les probabilités normales
Étapes
Exemple
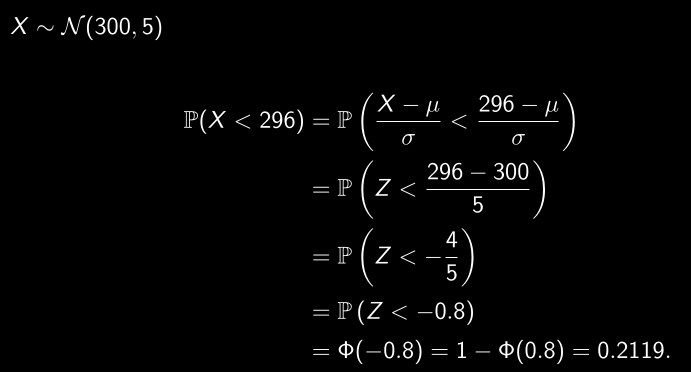=C'est pas 300, 5 mais 300, 5²!.
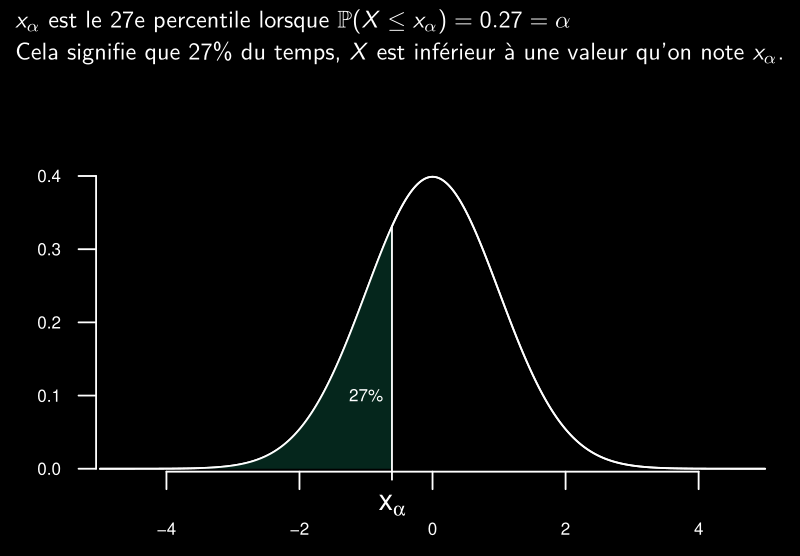
Percentiles
Exemple des scores SAT
Les scores SAT sont normalement distribués avec une moyenne µ = 500 et un écart-type σ = 100. Quel score SAT devez-vous obtenir pour être dans le 60e percentile ?
Résolvez le problème à l’envers.
On utilise alors l’inverse de la fonction cumulative de densité de la standard normale, Φ−1 (p), où Φ−1 (p) correspond à la valeur Z tel que Φ(Z ) = p.
Regarder dans le tableau
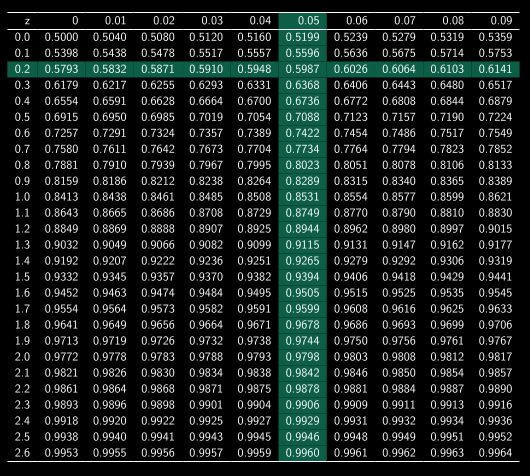
Déstandardiser
