Combinaisons
Exemple : création d’un examen
Nous avons un ensemble de :
- 15 questions vrai/faux (V/F) et 20 questions à choix multiple.
Question : Nous voulons créer un examen avec 10 questions dont exactement 4 sont V/F. Combien d’examens avec exactement 4 questions V/F peuvent être construits ? Remarque : Ignorez l’ordre des questions.
Nous avons un ensemble de 15 questions vrai/faux et 20 questions à choix
multiple. Parmi les examens avec 10 questions, quelle est la probabilité de choisir un examen avec 4 questions V/F (et 6 questions à choix multiple) ? Rappel de la définition classique de la probabilité :
Exemple : lancer d’une pièce équilibrée
Exemple : lancer d’une pièce déséquilibrée
Exemple: lancer d’une pièce déséquilibrée 2
Distribution binomiale
Expérience binomiale :
- n essais.
- Les essais sont indépendants.
- Deux issues possibles P( Succès ) = p.
- Probabilité binomiale.
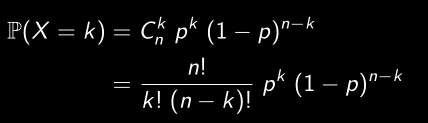
Le tiroir à chaussettes
- Un tiroir contient 6 chaussettes rouges et 4 chaussettes noires. Quelle est la probabilité de sélectionner 2 chaussettes rouges lorsque vous en tirez 5 du tiroir (avec remise) ?
- Il y a 5 essais.
- Chaque tirage est indépendant des autres, puisque nous choisissons une chaussette à chaque fois avec remise.
- Comme nous sommes intéressés à sélectionner des chaussettes rouges, nous appelons cela un succès et sélectionner une chaussette noire est un échec.
- Pour chaque essai, la probabilité de succès est p = 6/10 = 0, 6, elle est constante.
- Ceci est une expérience binomiale.
Prendre la route la plus courte
450 étudiants suivent le cours Introduction à la Statistique, mais la probabilité qu’un étudiant ne soit pas endormi à la fin d’un cours est de 0.01. Quelle est la probabilité qu’au moins un étudiant ne soit pas endormi à la fin du cours ?
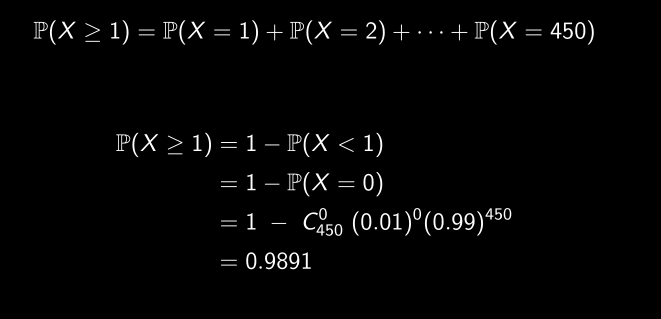
Distribution binomiale (n = 1)
Espérance et variance de W
Espérance de W
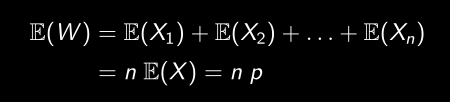
Variance de W
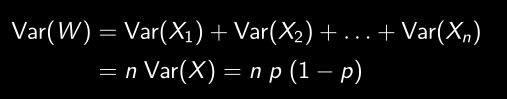
Loi binomiale : espérance et variance
- X ∼ Bin(n, p)
- Fonction de Masse de Probabilité (FMP):
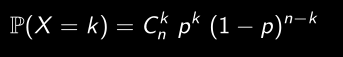
- Espérance:
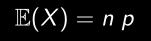
- Variance:
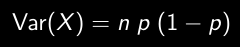
- Écart-type:
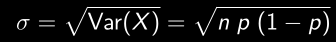
Variable aléatoire discrète
Variables aléatoires continues
Exemples
Discrètes vs continues
Une variable aléatoire U
Longueur d’un intervalle
