Espérance
Interprétations :
- Une moyenne pondérée par les probabilités.
- La moyenne à long terme de X.
- La valeur juste d’un pari.
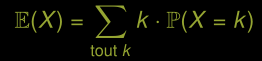
- Le point d’équilibre pour un histogramme ou un diagramme en barres de probabilité.
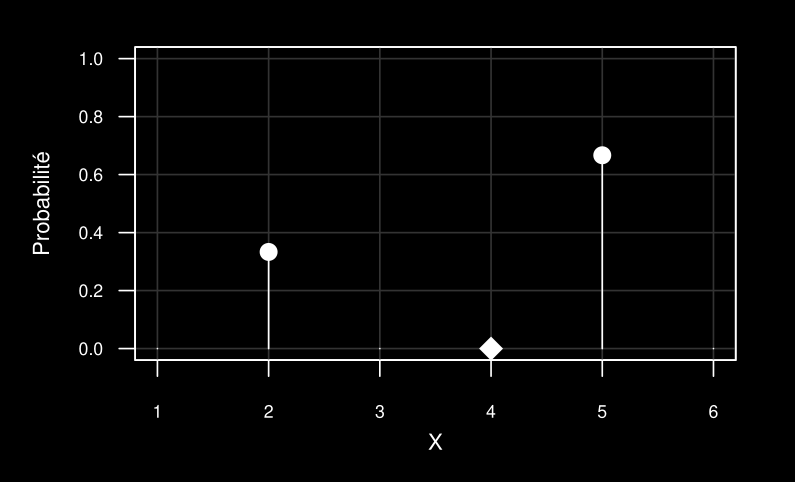
Formule
Calcul
C’est une moyenne pondérée des valeurs de X , où les poids correspondent aux probabilités associées à ces valeurs.
Exemple: pari équitable
Vous payez 100 CHF pour un pari:
- Si vous gagnez, vous recevez 210 CHF, et si vous perdez, vous recevez 0 CHF.
- X = votre gain/perte→
- X = 110 CHF, si vous gagnez.
- X = −100 CHF, si vous perdez.
- Supposons que les probabilités de gagner/perdre sont:
Ce pari est-il équitable?
La fonction de masse de probabilité (FMP) de X est :
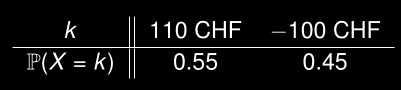Pour vérifier si le pari est équitable ou non, calculez l’espérance de votre gain/perte :
Donc?
Ce n’est pas un pari équitable, puisque l’espérance n’est pas nulle… mais devriez-vous jouer ?
- Oui, puisqu’on a l’avantage. Si on joue un grand nombre de fois (1000 fois par exemple) on gagnera 15.5 CHF.
Un autre exemple: Qui veut gagner des millions?
- Quitter = 100 000 CHF.
- Bonne réponse X = 250 000 CHF.
- Mauvaise réponse X = 32 000 CHF.
Deux cas
Choisir au hasard parmi les 4 réponses possibles
Utiliser l’option 50-50, et choisir au hasard entre 2 réponses
Mais
On va jouer qu’une fois, dans ce cas l’espérance n’est peut-être pas la meilleure manière de décider quoi faire. En plus ce modèle ne prends pas en compte le risque, il y a des gens que même avec une espérance plus faible vont prendre ce pari pour s’assurer (avec un risque plus faible) qu’ils gagnent une certaine quantité d’argent.
Ajout d’une constante
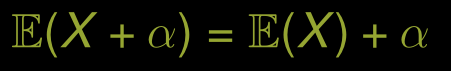On a un pari et X est la quantité gagnée et 10 CHF nous sont donnés en plus. Donc a=10 CHF, c’est une constante dont on est sûrs du sort.
Fonctions d’une variable aléatoire
Il est impossible d'obtenir par exemple un 18 puisque c’est une moyenne pondérée→ il faut faire attention aux résultat qu’on obtient.
Doubler la valeur de X
Multiplication par une constante
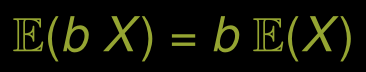
Propriétés de E(X)
Soit X et Y des variables aléatoires et a1, a2, b1 et b2 des constantes:
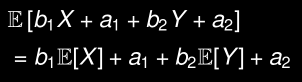
Exemple: dé bleu et dé vert
Deux dés équilibrés sont lancés, un bleu et un vert.
Déterminez l’espérance de Y et l’univers pour chaque dé bleu ou vert est:
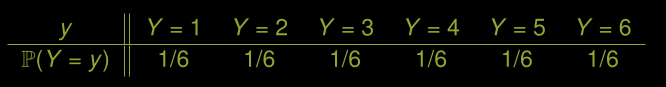
Mesurer la variabilité
La variance = Mesure de l’étendue de la FMP.
La variance = Espérance de la distance au carré de l’espérance.
Remarque
Comment calculer Var(X)
La variance ne peut jamais être négative, tout comme une probabilité. Si on a une variable aléatoire avec un seul valeur elle peut être 1 néanmoins.
Écart type
L’écart type est bien plus facile à interpreter que la variance.
Propriétés
Événements indépendants
Si A et B sont indépendants:
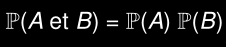
Lancers de pièces équilibrées
Et compter les piles
4 possibilités pourr X=1.
Univers
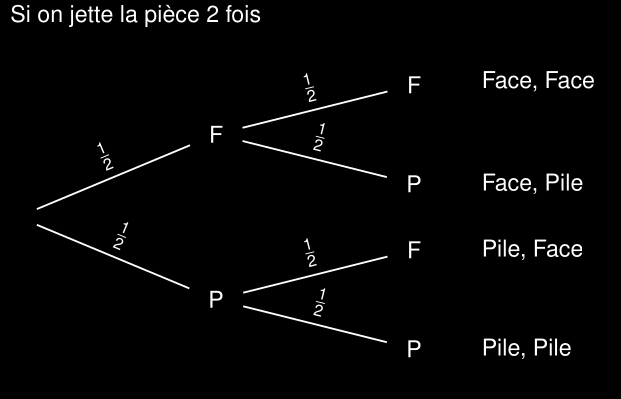==(1/2)²=1/4== = P(X=1).
Si on jette la pièce 4 fois
En général
Comment comptons-nous ces combinaisons?
Principe fondamental du comptage
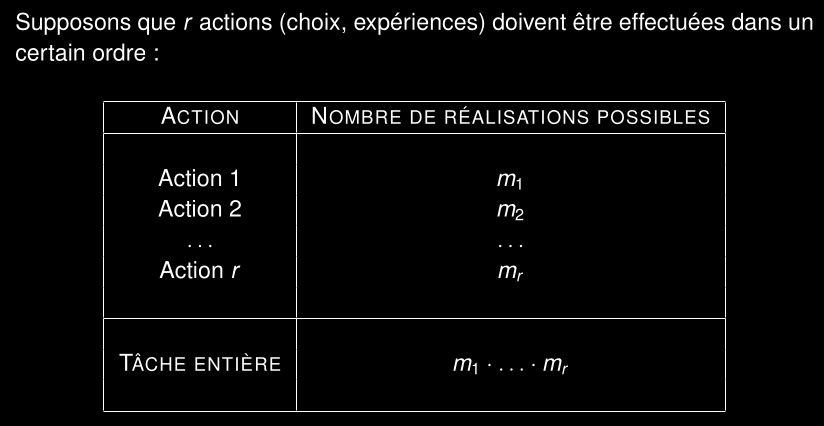
Choisir un ordre
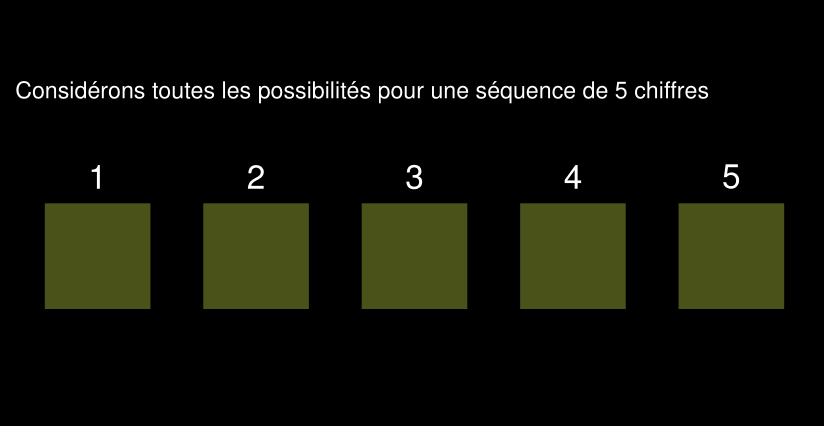
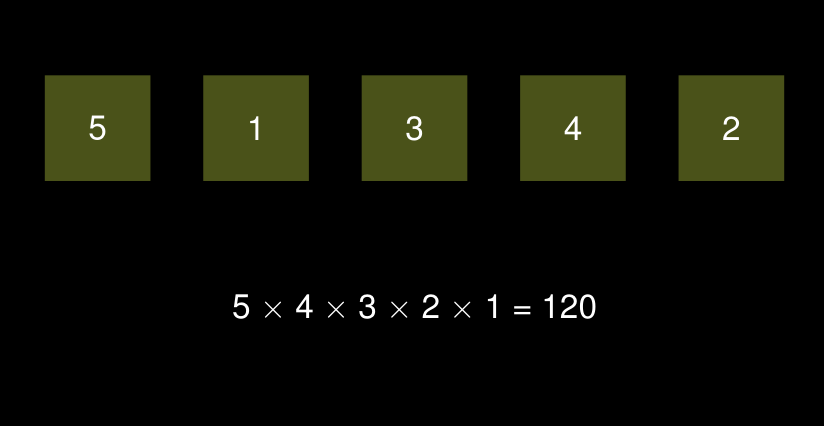
Comptage des séquences
Exemple: séquence (sans ordre)
Pourquoi entre 2? Parce que l’ordre n’a pas d’importance et donc la moitié des équipes est la même que l’autre.
k parmi n
Probabilité d’obtenir 6 faces sur 10 lancers
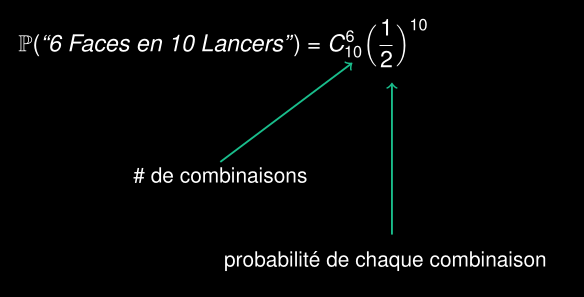
Suite d’événements indépendants
Autres probabilités
Expérience binomiale
Exemple: votation d’une loi
Probabilité binomiale
Distribution binomiale
