Indépendance et variables aléatoires
Règles de probabilité
Probabilité conditionnelle de A sachant B
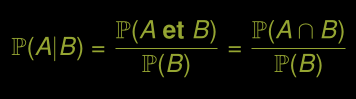
Et de B sachant A
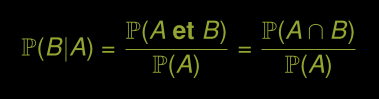
Règle de multiplication
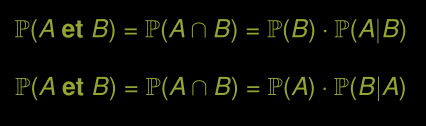
Règle générale d’addition
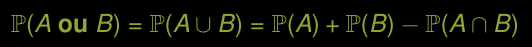
Probabilité totale
Règle du complément
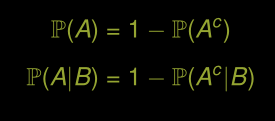
Exemple
Utilisez la règle générale de l’addition :
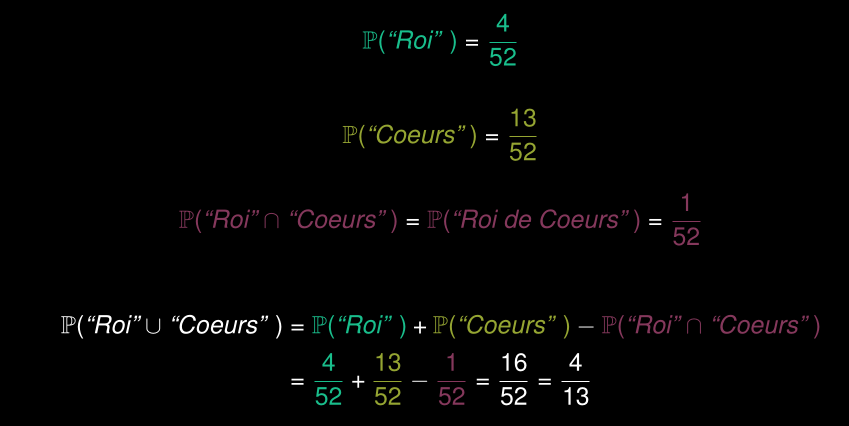
Exemple 2
Considérons un dé équilibré. Quelle est la probabilité de lancer un nombre pair ou un 3 ?
Indépendance
A et B sont des événements indépendants si:
Remarques
- Probabilité jointe de deux événements indépendants:
Indépendance: Roi et Coeur
Une autre façon de vérifier l’indépendance
Indépendance: Figure et Roi
Une autre façon de vérifier l’indépendance
Événements mutuellement exclusifs vs événements indépendants
Règles de base
- Non → 1 – Probabilité.
- Ou et Événements mutuellement exclusifs → Additionner.
- Et et Indépendance → Multiplier
Événements successifs
- A= Lancer Face 6 fois
- B= Obtenir FPFPPF
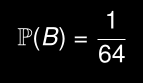
Échantillonnage sans remplacement
Un bocal contient 6 billes bleues et 6 billes rouges. Vous en tirez 3:
Tirer deux cartes d’un jeux standard:
- A = Première carte est un Roi.
- B = Deuxième carte est un Roi.
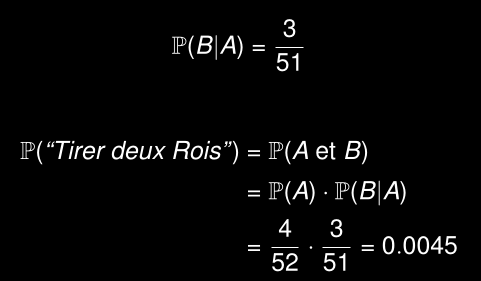
Variables aléatoires
Une variable aléatoire est une variable dont la valeur dépend de l’issue d’un
phénomène aléatoire. Chaque issue correspond à un nombre ou à un état/condition :
Nommons la variable aléatoire X:
Lancer une pièce équilibrée 3 fois
Résultats possibles:
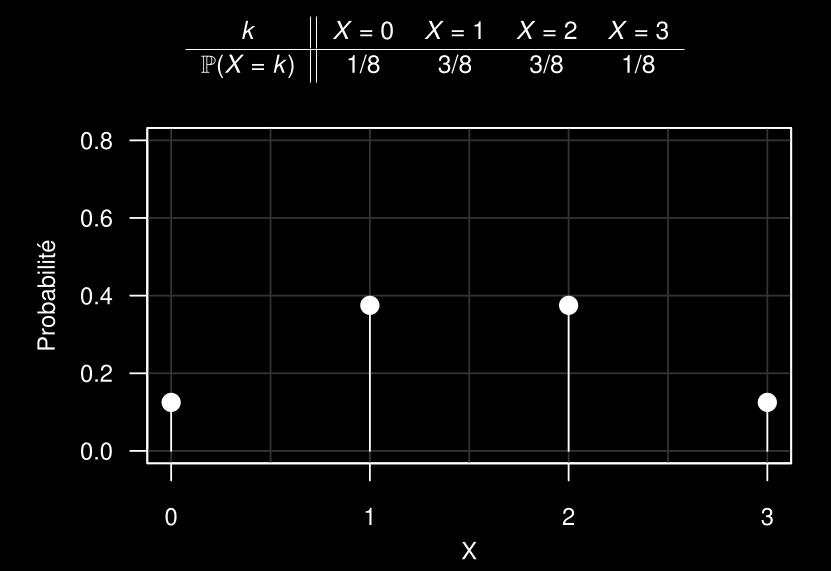
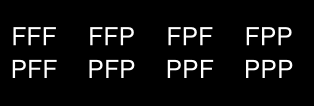X= Nombre de faces (F).
FMP: Fonction de masse de probabilité
Plus généralement
X prend des valeurs:
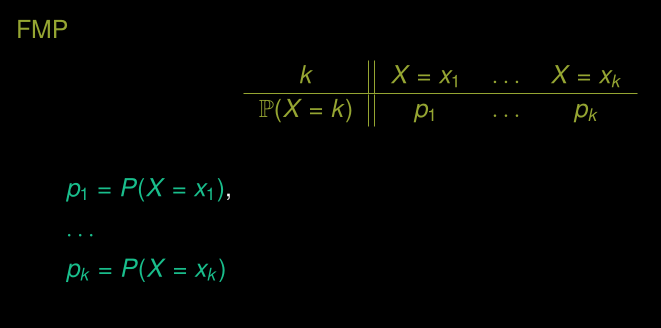
Remarques
Résultats
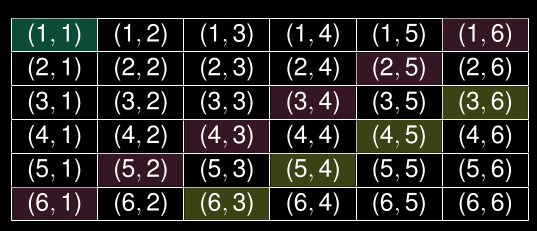
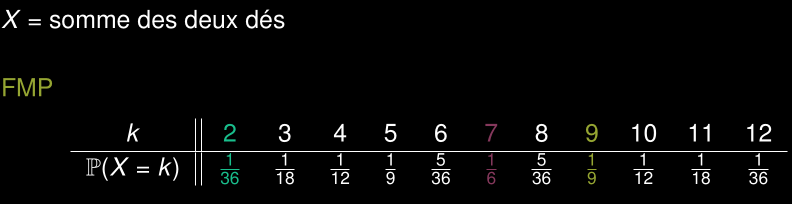
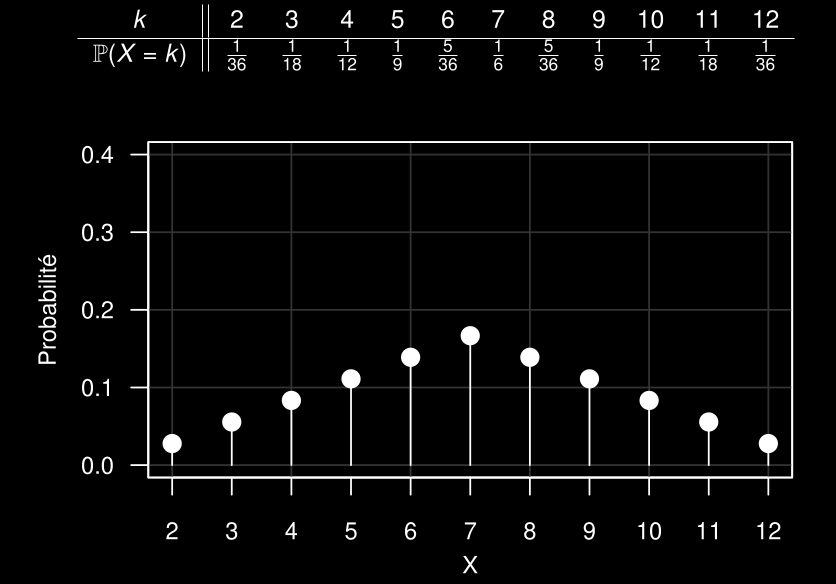
Événement A= {X=k}
Entretien d’embauche
On choisi 5 personnes au hasard dans une salle de 100 personnes. Parmi ces 100 personnes, 50 personnes étudient à Genève et 50 personnes étudient à Lausanne.
X = nombre de personnes sélectionnées qui étudient à Genève.
On obtient la distribution de probabilité suivante (nous verrons comment obtenir ces chiffres par la suite) :
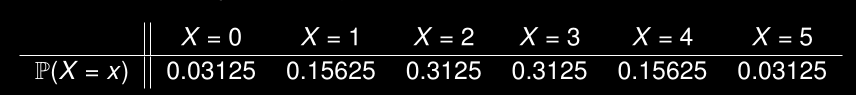
Quelle est la probabilité que un ou deux personnes sélectionnées étudient à Genève?
Quelle est la probabilité qu’==au moins 2== personnes selectionnées étudient à Genève?
Notation Sigma
Une abréviation pour écrire de longues sommes:
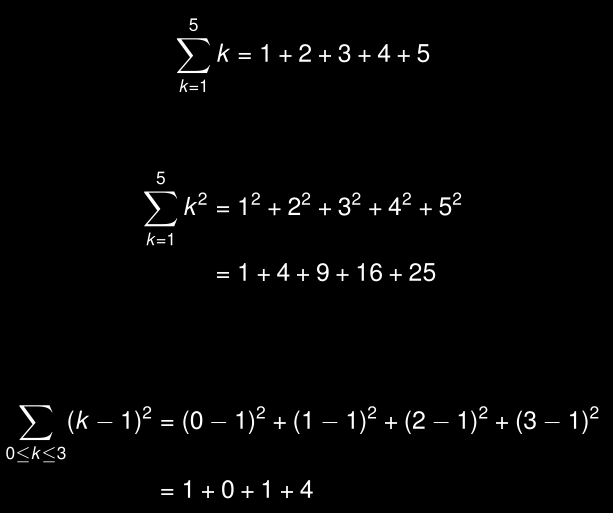
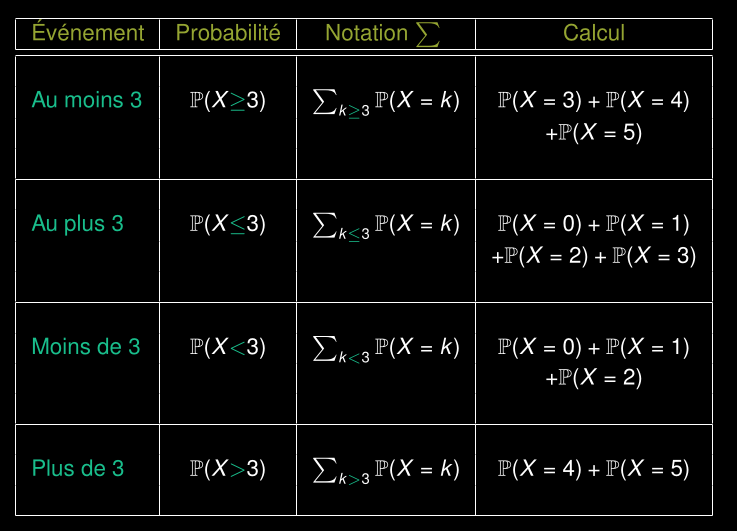
Formule fondamentale de la probabilité
- X= variable aléatoire.
- A= un ensemble des valeurs possibles de X (un événement).
Exemple de l’entretien d’embauche
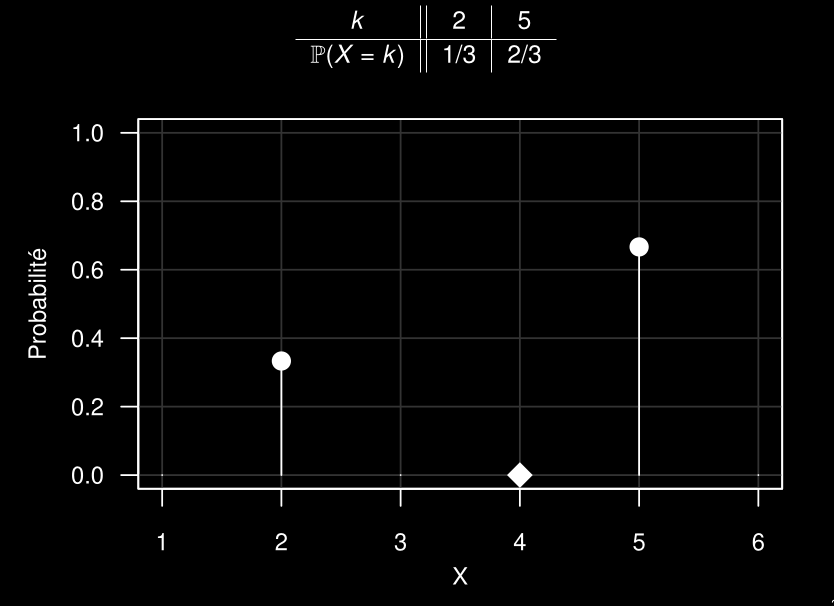
Exemple
- Supposons que nous avons la distribution suivante:
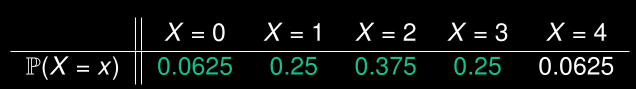
- Nous voulons calculer la probabilité suivante:
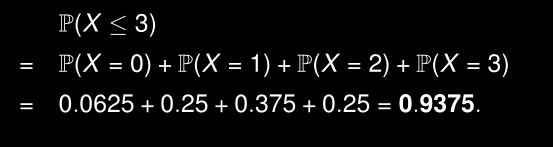
Espérance
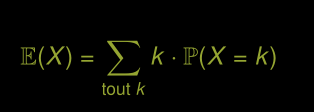
Interprétation
- Une moyenne pondérée par les probabilités.
- La moyenne à long terme de X.
- La valeur juste d’un pari.
- Le point d’équilibre pour un histogramme ou un diagramme en barres de probabilité.
Comment calculer E(X)
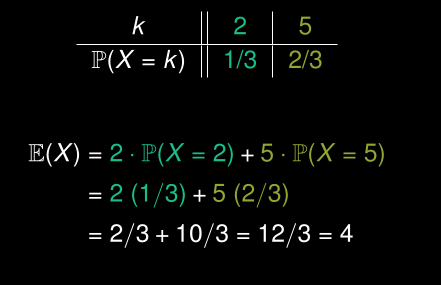
E(X)
