Séance 10-Test-Z, test-t et test-Z à deux échantillons

Test-Z, test-t et test-Z à deux échantillons

Exemple : test-Z

• Une entreprise de production de batteries affirme que la durée de vie moyenne de ses batteries de type A est de 100 heures.
• Un ingénieur souhaite vérifier cette affirmation. Il prélève un échantillon aléatoire de 100 batteries de type A et observe une durée de vie moyenne de 99.1 heures.
• On considère la durée de vie de chaque batterie comme indépendante. Il estime ensuite l’écart-type de la population avec l’écart-type de l’échantillon s qui est de 5.
• Il souhaite déterminer, au seuil de signification de 5%, si les données fournissent des preuves que la durée de vie moyenne des batteries de type A diffère de 100, ou si l’écart observé peut simplement être dû au hasard.

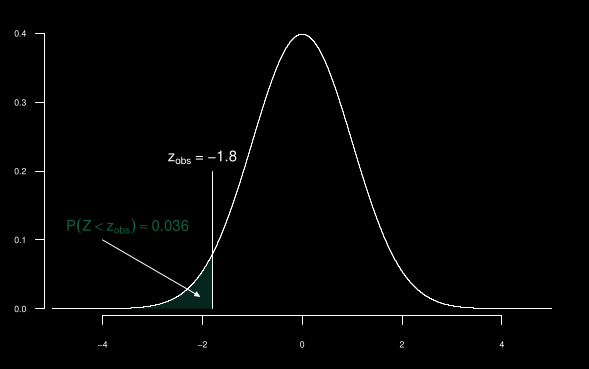
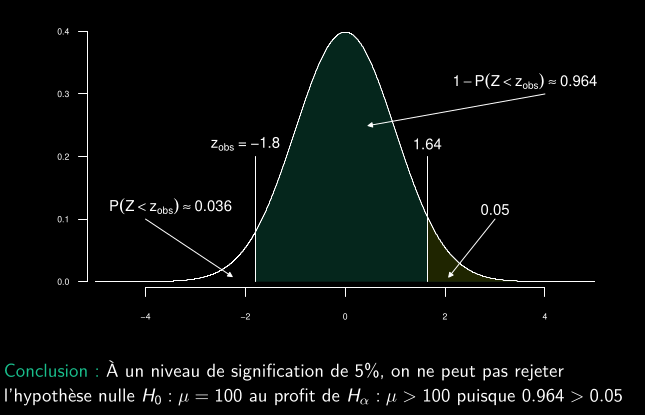
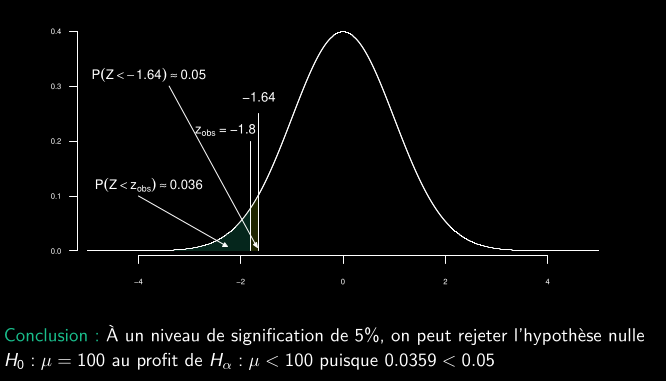
Exemple : Test-t

• La même entreprise de production de batteries affirme que la durée de vie moyenne de ses batteries de type B est de 50 heures.
• Un ingénieur souhaite vérifier cette affirmation. Il prélève un échantillon aléatoire de 10 batteries de type B et observe une durée de vie moyenne de 47.1 heures. On considère la durée de vie de chaque batterie de type B comme indépendante et distribuée normalement.
• Il estime ensuite l’écart-type de la population avec l’écart-type de l’échantillon s qui est de 4.5.
• Il souhaite déterminer, au seuil de signification de 5%, si les données fournissent des preuves que la durée de vie moyenne des batteries de type B diffère de 50, ou si l’écart observé peut simplement être dû au hasard.
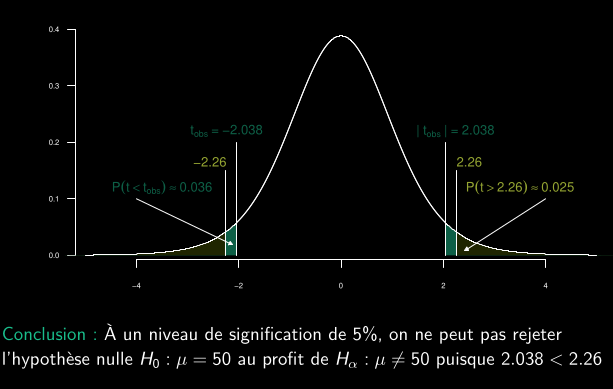
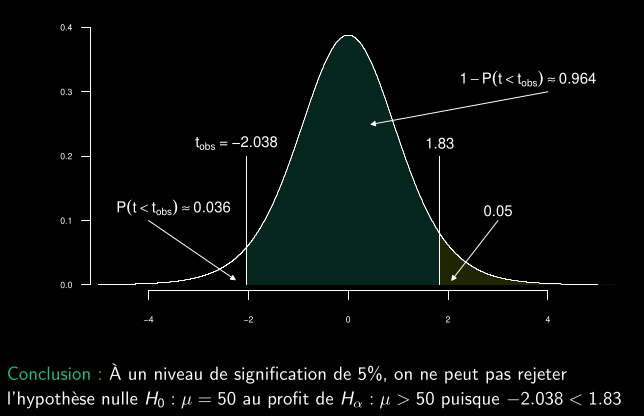
• Un second ingénieur pense que la moyenne de la population est supérieure à 50 heures et souhaite tester les hypothèses suivantes :
  • H0 : µ = µ0 = 50.
  • Hα : µ > 50.
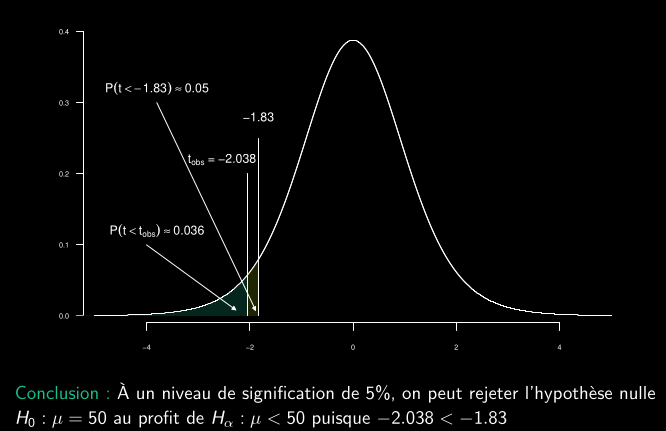
• Un troisième ingénieur pense que la moyenne de la population est inférieure à 50 heures et souhaite tester les hypothèses suivantes :
  • H0 : µ = µ0 = 50.
  • Hα : µ < 50.

Tests à deux échantillons

• Il est courant de vouloir déterminer des différences entre deux groupes. Par exemple :
  • En médecine : comparer un traitement à un placebo.
  • En économie : comparer deux politiques publiques.
  • Dans l’industrie : comparer les performances entre deux machines.
• Objectif statistique : déterminer si les différences observées sont dues au hasard - ou à un effet réel.
• On considère deux échantillons indépendants, chacun provenant d’une des deux populations. Ces échantillons ne sont pas nécessairement de même taille.
• On fait un test pour déterminer si les moyennes des populations sont les mêmes.

Exemple

• L’entreprise de production de batteries possède deux chaînes de production pour les batteries de types A. On voudrait tester si la durée de vie des batteries diffère en fonction de la chaîne de production.
• Un échantillon aléatoire de 80 batteries de la chaîne de production 1 et un échantillon aléatoire de 70 batteries de la chaîne de production 2 sont prélevés.
• On suppose que les observations sont IID et que les groupes sont indépendants.
• Chaîne de production 1 : X̄1 = 99.3 heures, s1 = 4.7, n1 = 80.
• Chaîne de production 2 : X̄2 = 100.8 heures, s2 = 5.4, n2 = 70.
• On souhaite déterminer, au niveau de signification de 5%, si les données fournissent des preuves que la durée de vie moyenne des batteries issue de la chaîne de production 1 (µ1 ) diffère de celle issue de la chaîne de production 2 (µ2 ), ou si l’écart observé peut simplement être dû au hasard.

Test-Z à deux échantillons

Retour sur le dernier exemple

Exemple : test d’un médicament

Calcul du test-Z unilatéral

Randomisation

• Reprenons l’exemple du médicament et supposons que
  • le choix de recevoir le traitement ait été fait directement par la personne concernée
  • ou que le traitement ait été prescrit en priorité aux situations les plus graves par le personnel soignant.
• Problème : les groupes pourraient différer systématiquement avant même le traitement.
• Le médicament semble efficace, mais cet effet pourrait venir d’un biais de sélection.
• Solution : l’assignation aléatoire (randomisation) garantit que les différences observées sont dues, en moyenne, au traitement.

Que faire si les échantillons sont petits?

• Lorsque les échantillons sont petits, et que la normalité est douteuse, d’autres tests peuvent être utilisés.
• Par exemple : le test-t à deux échantillons, le test de Welch (en cas de variances inégales), ou le test de Wilcoxon (non paramétrique).
• Ces tests ne sont pas abordés ici, mais l’idée générale reste la même : utiliser une statistique de test pour décider si les données sont compatibles avec l’hypothèse nulle H0.

D’autres tests à deux échantillons? Ou plus?

• On peut aussi effectuer des tests à deux échantillons pour :
  • Des proportions.
  • Des variances.
• Il aussi possible d’effectuer des tests pour comparer les moyennes de plus de deux échantillons/groupes, mais… attention ! !

Exemple : les jelly beans provoquent-ils l’acné?

Multiplier les tests peut être dangereux!

• La p-valeur est une quantité aléatoire, car elle dépend des données échantillonnées.
• Il peut donc arriver, par hasard, qu’une p-valeur soit inférieure au niveau de signification choisi, même si H0 est vraie et ne devrait pas être rejetée. Au niveau de signification de 5%, cela signifie qu’en moyenne, même sans effet réel, la p-valeur sera inférieure à 5% une fois sur vingt.
• Lorsque plusieurs hypothèses sont testées, la probabilité d’observer un tel événement (rare) augmente. Ainsi le risque de commettre une erreur de type I, i.e., de rejeter à tort H0 , augmente lui aussi.
• Faire plusieurs tests, sur les mêmes données ou sur des données différentes, est donc risqué (et pourtant très courant), car cela produit presque automatiquement des résultats “significatifs” même en l’absence d’effet réel.
• Des solutions pratiques existent, comme l’ajustement du niveau de signification en fonction du nombre de tests effectués.

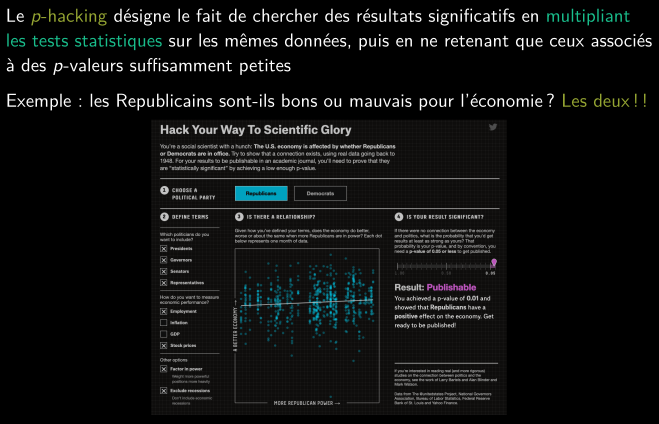
p-hacking

HARKing

• Le HARKing est l’acronyme de “Hypothesizing After the Results are Known” désignant les pratiques de recherche questionnables. Cette dérive peut être définie comme le fait de faire passer des hypothèses a posteriori comme des hypothèses a priori.
• En pratique ?
  • Tester si une couleur de jelly bean est liée à l’acné (tests multiples).
  • Prétendre que c’était l’hypothèse origniale.
  • Publier cette découverte majeure ! ! !

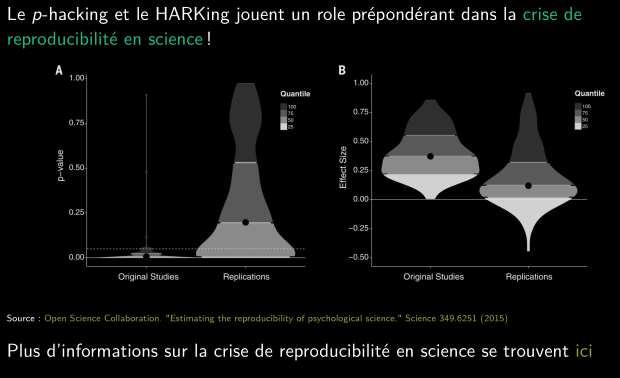
Conséquence du p-hacking & du HARKing

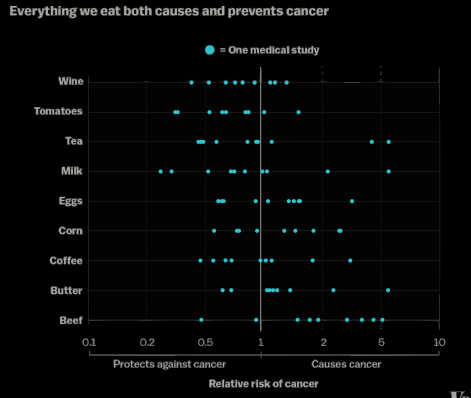
Pour conclure

• Toute analyse basée sur des échantillons de données est soumise à de l’aléatoire Avec les données, il n’y a jamais de certitude à 100 %, mais plutôt une conclusion associée à un risque (estimé) que cette conclusion soit erronée.
• Il est nécessaire de s’y habituer, et tout résultat scientifique affirmant une validité à 100 % sur la base de données est tout simplement incorrect.
• En revanche, bien contrôler le risque statistique et formuler correctement les conclusions que l’on peut tirer d’une analyse de données peut réellement permettre d’apporter de nouvelles connaissances, en particulier dans toutes les sciences fondées sur des observations/expérimentations.

UNIGE Intro-stat