Concepts clés en probabilité
Modélisation des phénomènes aléatoires
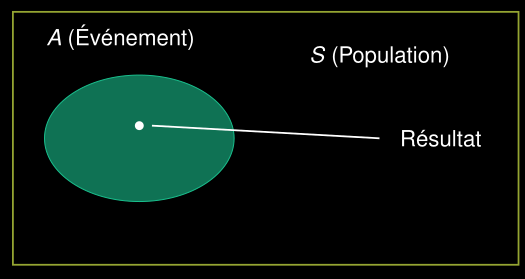
Résultats
Résultats possibles d’une expérience.
Population
Ensemble de tous les résultats possibles (noté S).
Événement
Ensemble de résultats (par exemple, A dans l’illustration).
Exemple: lance d’un dé équilibré
 Si le dé est équilibré, alors la probabilité d’obtenir chaque face est la même, c’est-à-dire:
Si le dé est équilibré, alors la probabilité d’obtenir chaque face est la même, c’est-à-dire:
- Probabilité (un) = Probabilité (deux) = Probabilité (trois) = Probabilité (quatre) = Probabilité (cinq) = Probabilité (six)
- ou, en d’autres termes→
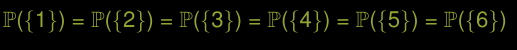
Exemple: lancer d’une pièce équilibrée

Probabilité
Si tous les résultats sont équiprobables, c’est-à-dire qu’ils ont la même probabilité de se produire:
 Ceci ne marche qu'avec des résultats équiprobables
Ceci ne marche qu'avec des résultats équiprobables
Exemple: lancer d’un dé équilibré
- Quelle est la probabilité d’obtenir un 5 ?
- Quelle est la probabilité que le dé tombe sur un nombre impair ?
Nous pouvons utiliser la définition classique de la probabilité, car tous les nombres d’un dé ont la même probabilité d’apparaître, puisque c’est un dé équilibré.
Étapes
- Déterminer l’univers, qui sont les résultats possibles d’un tirage de dé :

- Déterminer les événements qui nous intéressent :

- Calculer la probabilité en utilisant la définition :

Exemple: lancer une pièce équilibrée trois fois
Probabilité d’obtenir 3 faces :
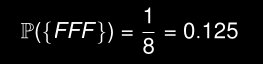 Résultats :
Résultats :
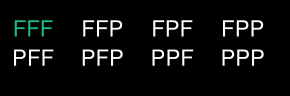
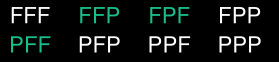
Probabilité d’obtenir 2 faces
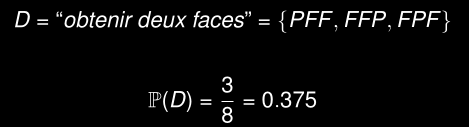 Résultats :
Résultats :
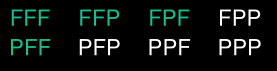
Probabilité d’obtenir au moins 2 faces
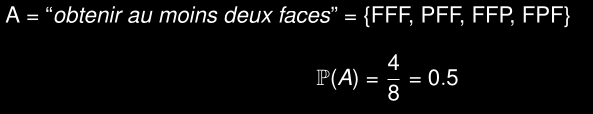 Résultats :
Résultats :
Propriétés des probabilités
- Pour tout événement A:
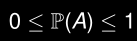
- Un événement qui a une probabilité de 1 est appelé certain.
- Un événement qui a une probabilité de 0 est appelé impossible (du point de vue probable ça n’arrive jamais).
Complément/Événements opposés
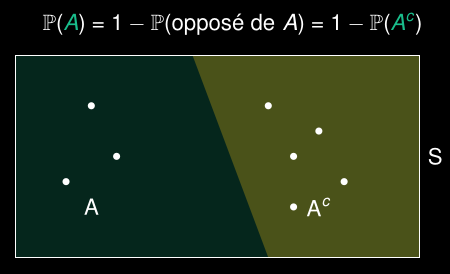 ==La P de A+la P que A n’arrive pas est toujours = 1==
==La P de A+la P que A n’arrive pas est toujours = 1==
Exemple : lancer un dé équilibré

Événements mutuellement exclusifs
Lorsque les événements A et B (notés par A ∩ B) ne peuvent pas se produire simultanément (noté par A ∩ B = ∅), alors ils sont appelés événements mutuellement exclusifs. Leur somme peut-être inférieure/égale à 1.
Exemples
- Élections :

- Lancer une pièce :

- Lancer un dé équilibré :

Illustration par Venn
Si A et B ne peuvent pas se produire simultanément :
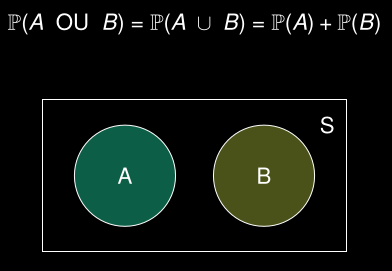 A et B n’ont aucun élément en commun!
A et B n’ont aucun élément en commun!
Ensembles
 ==On ne peut pas faire P=A+B si A et B se croisent comme dans le premier ensemble, puisqu’on compterait la partie complémentaire deux fois==.
==On ne peut pas faire P=A+B si A et B se croisent comme dans le premier ensemble, puisqu’on compterait la partie complémentaire deux fois==.
Probabilité conditionnelle
Lancez un dé équilibré et quelqu’un nous dit que le résultat du dé est un nombre impair.
- Quelle est la probabilité que le résultat soit un cinq étant donné que le résultat du dé est un nombre impair ?
- Et la probabilité d’obtenir un 6 étant donné que le résultat du dé est un nombre impair ?
Probabilité conditionnelle de l’événement B étant donné que l’événement A est survenu :
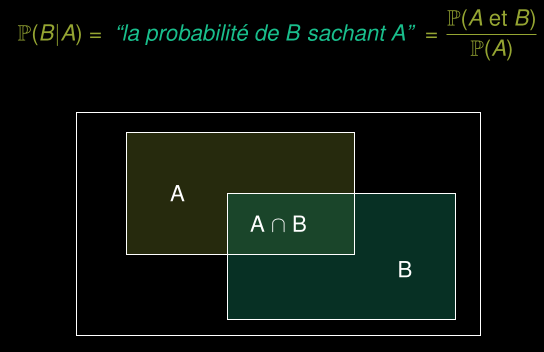
Probabilité conditionnelle de l’événement B étant donné que l’événement A
est survenu. Si les résultats sont équiprobables :
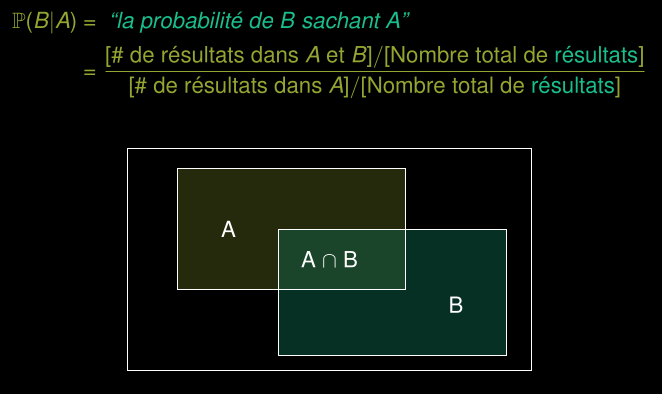
Probabilité conditionnelle de l’événement B étant donné que l’événement A
est survenu :
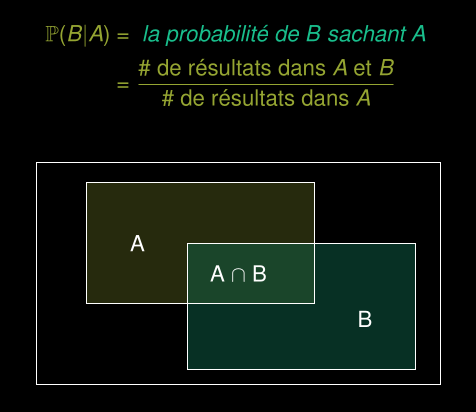
Exemple
Quelle est la probabilité que le résultat d’un lancer de dé équilibré soit cinq
étant donné que le résultat est un nombre impair ?

Autre exemple
Si vous savez qu’une famille a deux enfants et que l’un d’eux est un garçon, quelle est la probabilité que l’autre enfant soit également un garçon ?
- Population = ensemble des paires possibles d’enfants

- La probabilité que les deux enfants soient des garçons étant donné qu’il y a au moins un garçon est:
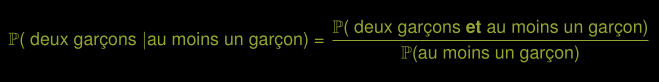

En général
- P(A|B) = probabilité conditionnelle de A sachant B.
- P(B|A) = probabilité conditionnelle de B sachant A.
Exemple

Probabilité jointe
P(A et B) = probabilité jointe de A et B la probabilité que les événements A et B se produisent ensemble (A ∩ B).
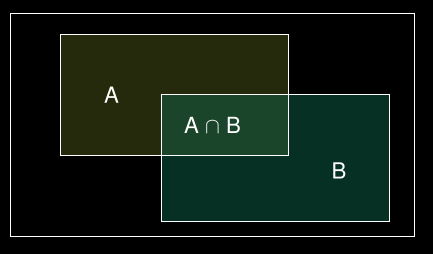
Règles de probabilité
Probabilité conditionnelle de A sachant B
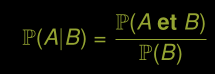
Probabilité conditionnelle de B sachant A
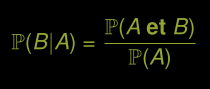
Règle de multiplication
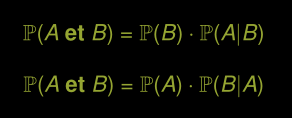
Règle générale d’addition
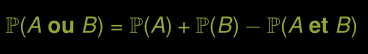
Probabilité totale
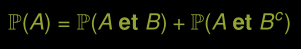
Règle du complément
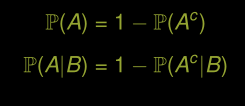
Deux types de questions

Exemple test covid
- 1 % des étudiants ont le COVID.
- Le test de dépistage est précis à 99 %. (Ainsi, il y a 1 % de chance que le test ne soit pas précis).
- Léa (une étudiante) est testée positive au COVID.
Quelle est la probabilité que Léa ait effectivement le COVID étant donné qu’elle a été testée positive ?



