Séance 20,21-Les décisions en incertitude

Décisions en incertitude

Économie de l’aversion au risque

• En général, les gens n’aiment pas le risque et sont prêts à débourser de l’argent pour l’éviter.
• On dit de quelqu’un qui est frileux au risque qu’il est risquophobe.
• Mais qu’entend-on exactement par risque? Et pourquoi les gens ne l’aiment-ils pas?
• Pour répondre à ces questions, nous devons au préalable nous intéresser au concept de valeur espérée et du sens donné au mot incertitude.

Les aléas de la vie

• Une variable aléatoire est une variable dont la valeur future est incertaine.
• Par exemple, les dépenses en santé pour l’année à venir.
• Si l’on suppose que la personne a une chance sur deux de tomber malade et que les dépenses de santé se concrétiseront.
• Supposons que les dépenses pour cette maladie sont connues et se montent à 10’000 CHF.

Anticipations et incertain

• La valeur espérée d’une variable aléatoire est la moyenne pondérée de toutes les valeurs possibles, où les poids de chaque valeur correspondent aux probabilités associées aux valeurs de leur état respectif.
• Dans notre exemple, la valeur espérée des dépenses de santé est:
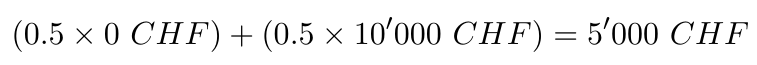
• On peut faire l’analogie avec une moyenne: on ne subit jamais un coût de 5’000 CHF, mais c’est une sorte d’alternance entre des dépenses de 0CHF et de 10’000 CHF.

Incertain et espérance

• Pour en déduire une formule générale de la valeur espérée d’une variable aléatoire, nous imaginons qu’il y a un certain nombre d’états de la nature différents, chacun pouvant se produire avec une certaine probabilité.
• Un état de la nature 𝑆𝑖 est un événement futur possible ayant une probabilité 𝑝𝑖.
• Par conséquent, la valeur espérée VE de la variable aléatoire peut s’écrire:

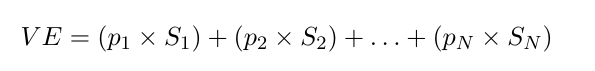
Espérance et risque

• Le risque se compose de l’incertitude concernant l’état futur d’une variable. En général, toutes choses égales par ailleurs, les gens préfèrent réduire le risque.
• On se concentre sur le risque financier où l’incertitude entoure des résultats monétaires pour simplifier l’analyse. Dans notre exemple, on risque de tomber malade, mais nous nous intéressons uniquement aux dépenses de soins associées et non à la perte de bien-être liée à la maladie.
• Comment expliquer que les gens n’aiment en général pas le risque?

Aversion au risque

• La réponse à cette question repose sur le concept d’utilité marginale décroissante.
• Pour comprendre comment l’utilité marginale décroissante implique l’aversion au risque, reprenons l’exemple de la dépense potentielle de santé et comment elle affecte le revenu du ménage, que l’on suppose égal à 30’000 CHF.
• Le revenu espéré devient:

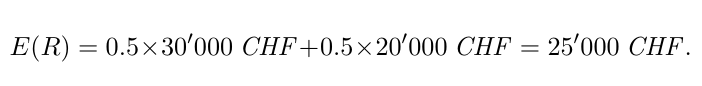
L’espérance d’utilité

• Le bien-être devient également incertain. L’utilité espérée correspond à la valeur espérée de l’utilité totale que l’individu retire d’événements futurs et incertains.
• Dans l’exemple, l’espérance d’utilité de ce ménage est moindre que si elle pouvait compter sur un revenu certain de 25’000 CHF, après des dépenses de santé connues à l’avance.
• L’utilité espérée est ce que les gens essaient de maximiser dans un environnement risqué.
• Pour des personnes risquophobes, l’utilité d’un montant fixe et certain est plus élevée que l’utilité espérée associée à la valeur espérée de ce même montant en incertitude.

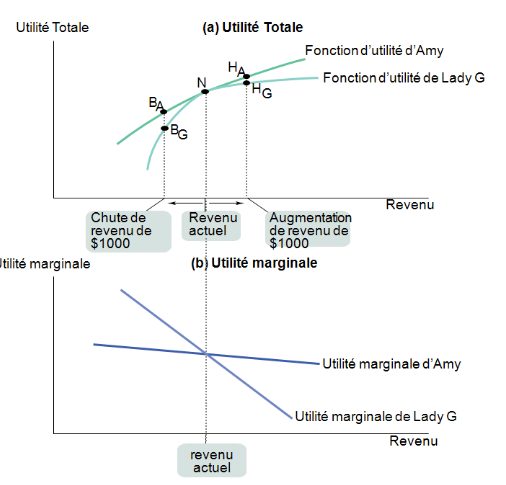
Utilité totale et utilité marginale d’un ménage risquophobe

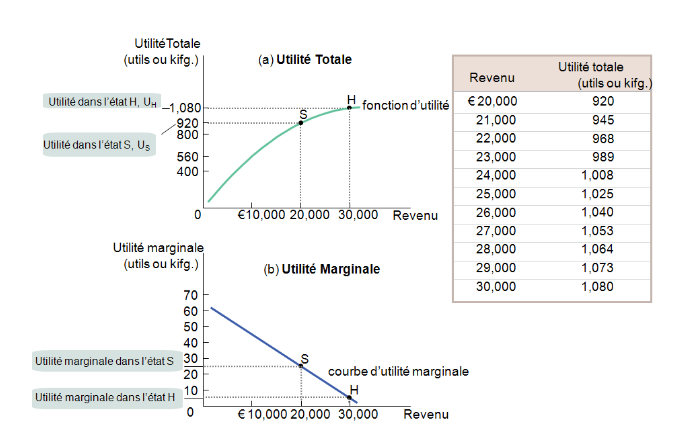
Principe de l’aversion au risque

• Dans la vraie vie, la plupart des gens sont risquophobes: Ils sont prêts à réduire le risque auquel ils sont confrontés, tant que le coût correspondant leur garantit une valeur espérée de leur richesse qui est inchangée.
• Ils sont donc prêts à payer une police d’assurance actuarielle pour laquelle la prime est égale à la valeur espérée du remboursement, et en fait même plus que ça.
• L’achat d’une police d’assurance actuarielle accroît l’utilité espérée, ce qui est dû au concept d’utilité marginale décroissante.
• La raison tient au fait qu’un franc gagné lorsque le revenu est bas ajoute plus de bien-être qu’un franc perdu lorsque le revenu est élevé.

Paradoxe de St. Pétersbourg

. Le mathématicien suisse Bernouilli a utilisé le principe d’utilité marginale décroissante pour résoudre le Paradoxe de St. Petersbourg (Cf. Wikipedia).

• Combien accepteriez-vous de miser pour le jeu suivant?
• L’espérance de gain de ce jeu est infinie!

L’effet d’une assurance actuarielle sur le revenu disponible d’une famille et son utilité espérée

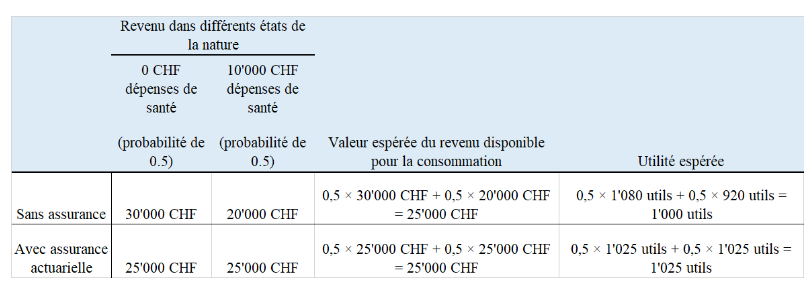
• L’utilité espérée d’avoir 25’000 CHF à chaque période est supérieure à l’utilité espérée d’avoir soit 30’000 CHF, soit 20’000 CHF.

Principe d’aversion au risque

• On voit donc que le fait d’être risquophobe tient à l’utilité marginale décroissante qui caractérise la plupart des personnes.
• Bien entendu, le degré d’aversion au risque varie entre personnes, avec certaines très risquophobes, d’autres seulement un peu.
• Les différences dans les préférences mais aussi dans les revenus ou dans les richesses produisent des différences dans les degrés d’aversion au risque.
• Plus la fonction d’utilité est concave, plus la personne est risquophobe.
• Plus la fonction d’utilité est proche d’une droite, moins la personne est risquophobe.

Payer pour éviter le risque

• Les différences observées dans l’aversion au risque comportent une implication importante: Elles déterminent le montant qu’un individu est prêt à payer pour éviter un risque.
• Une personne neutre au risque n’est pas du tout sensible au risque. Cette personne étant indifférente entre une situation risquée ou non, elle ne sera pas prête à payer quoi que ce soit pour éviter le risque.
• En fonction de l’importance de la prime, une personne risquophobe est prête à payer une prime plus élevée qu’une prime actuarielle.
• Plus grande est l’aversion au risque, plus la prime que la personne est prête à payer sera grande.

Risquophilie et neutralité au risque

• Jetez une pièce en l’air. Si c’est FACE, vous touchez 100 CHF et vous perdez 100 CHF si c’est PILE. Ce pari est actuariel avec une valeur espérée de: 𝑉 𝐸 = 0.5 × 100 + 0.5 × (−100) = 0.
• Joueriez-vous à ce jeu?
  • Les personnes risquophobes (utilité concave) ne joueront pas;
  • Les personnes neutres au risque (utilité linéaire) sont indifférentes entre jouer ou ne pas jouer;
  • Les personnes risquophiles prendront volontiers ce pari (utilité convexe).

Des loteries

• Les loteries sont-elles actuariellement justes? Pour y répondre, il faut examiner la valeur espérée du jeu. Prenons un exemple avec Swisslotto où l’on peut (selon les jours) gagner 1’000’000 CHF avec une probabilité de 1/5’245’786 par grille. Le prix d’une grille est de 2,50 CHF. La valeur espérée du jeu est:
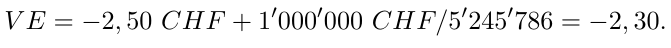
• Et pourtant, des millions de personnes (risquophobes) jouent régulièrement ce type de loteries et autres jeux ou paris actuariellement injustes…
• Théorie des perspectives (Kahneman & Tversky): les gens tendent à surestimer les petites probabilités et sous-estimer les grandes probabilités.

Acheter, vendre et réduire les risques

• Le secteur de l’assurance repose sur deux principes fondamentaux:
  1. L’échange de risques, comme l’échange de n’importe quel bien, peut générer des gains mutuellement avantageux.
     • Dans ce cas, le gain est réalisé lorsque des personnes peu enclines à supporter des risques transfèrent ces derniers contre rémunération à d’autres personnes moins sensibles au risque.
     • Typiquement, des investisseurs riches ont davantage de tolérance au risque que des ménages pauvres.
  2. Le second est qu’une partie du risque peut être réduite à travers la diversification.

La force de la diversification

• Deux événements possibles sont dits indépendants si l’un des deux n’a pas plus de chance de survenir lorsque l’autre se produit.
• En présence d’ événements indépendants, une stratégie de diversification peut sensiblement réduire le risque.
• Un agent peut diversifier en investissant dans des choses très différentes entre elles, de sorte que les pertes potentielles sont des événements indépendants.
• La diversification est facilitée par l’existence d’institutions telles les bourses, dans lesquelles les gens échangent des titres, comme des actions ou des obligations.

Comment diversifier?

• Une forme de diversification poussée, que mettent en place typiquement les assurances, consiste dans le groupement (pooling). Avec un groupement, chaque individu ne constitue qu’une petite portion d’une multitude d’événements indépendants.
• L’avantage du groupement est de baisser substantiellement le risque total.
• Imaginons un vendeur pouvant vendre 10 lunettes de soleil (prix=20 CHF) par beau temps et seulement deux par mauvais temps. De même, il peut vendre 20 parapluies (prix=10) s’il pleut, et seulement 4 s’il fait beau. Il pourrait aussi diversifier en vendant la moitié de chaque bien.

Les limites de la diversification

• Des événements sont corrélés positivement si chacun d’entre eux a plus de chances de se produire lorsqu’un autre se réalise aussi.
• Avec des événements corrélés positivement, il existe un risque systémique qui ne disparaîtra pas quel que soit le degré de diversification.
• Quelques exemples de risques financiers corrélés positivement que des investisseurs doivent affronter:
  • Mauvaise météo (pour l’agriculture).
  • Événements politiques.
  • Cycles conjoncturels.

UNIGE IntroMicroéconomie